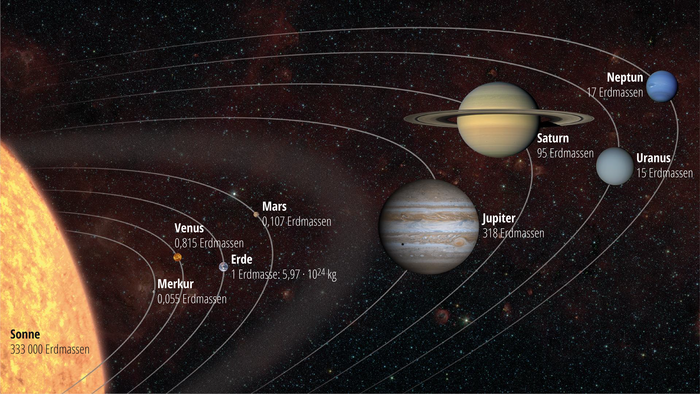
Wie wiegt man einen Planeten?

Wir stellen uns und allerlei andere Dinge einfach auf die Waage, um das Gewicht zu ermitteln. Die Masse eines Planeten lässt sich nicht ganz so leicht bestimmen.

Im Lauf der Zeit haben Menschen höchst unterschiedliche Arten von Waagen entwickelt – es gibt Federwagen, Balkenwaagen, Neigungswaagen und viele mehr. Das Grundprinzip ist jedoch bei allen identisch: Waagen messen die Gewichtskraft, die auf den daraufliegenden Körper wirkt. Da diese Gewichtskraft proportional zur Masse ist und die Proportionalitätskonstante bekannt – es handelt sich um die Fallbeschleunigung auf der Erde –, lässt sich aus der Gewichtskraft die Masse berechnen. Praktischerweise zeigen die Skala oder das Display der meisten Waagen nicht die Gewichtskraft in der Einheit Newton an, sondern bereits die Masse in Kilogramm.

Die Fallbeschleunigung variiert allerdings minimal von Ort zu Ort. Denn sie hängt nicht nur von der Anziehungskraft der Erde, sondern auch von der am jeweiligen Ort wirkenden Zentrifugalkraft durch die Erdrotation ab. Zudem ist der Planet keine exakte Kugel, sondern leicht abgeplattet. Und die Erdoberfläche ist nicht glatt, sondern weist mit Bergen und Tälern allerlei Unebenheiten auf. All das führt dazu, dass die Fallbeschleunigung nicht überall gleich groß ist. Doch im täglichen Leben spielen diese Unterschiede keine signifikante Rolle, da sie nur im Promillebereich liegen.

Neben Waagen kommt in der alltäglichen Praxis noch eine weitere Methode zum Einsatz, um Massen zu bestimmen: Die Messung über das Volumen, zum Beispiel mit einem Messbecher. Ist nämlich die Dichte eines Stoffes bekannt, so ergibt sich die Masse einfach aus dem Volumen, multipliziert mit der Dichte. Deshalb gibt es an Messbechern verschiedene Skalen für verschiedene Stoffe, die der jeweiligen Dichte angepasst sind. Während die beiden Messverfahren für allerlei Lebewesen und Gegenstände auf der Erde gut funktionieren, für Planeten und andere Himmelskörper im Weltall eignen sie sich nicht.

Newton und sein Gravitationsgesetz

Doch die Physik bietet auch hier eine Lösung. Die Grundlage dafür bildet das von Issac Newton entdeckte Gravitationsgesetz: Es beschreibt die Gravitation – also die Anziehungskraft –, die zwei Massen aufeinander ausüben. Newton zufolge ist die Kraft proportional zu den beiden Massen und umgekehrt proportional zum Quadrat des Abstands der beiden Massen. Verdoppelt man also beispielsweise eine der Massen – egal welche –, so verdoppelt sich auch die Anziehungskraft. Verdoppelt man dagegen den Abstand, so sinkt die Anziehungskraft nicht nur auf die Hälfte, sondern auf ein Viertel des ursprünglichen Werts.

Mit diesem Gesetz gelang es Newton im Jahr 1687, die Bewegung der Planeten im Sonnensystem erfolgreich zu beschreiben. Und auch das von Galileo Galilei beschriebene Gesetz des freien Falls ließ sich damit erklären. Die Fallbeschleunigung ist demnach proportional zur Erdmasse und umgekehrt proportional zum Quadrat des Erdradius. Da die Größe der Erde zu Newtons Zeit bereits gut bekannt war, ergab sich damit für Newton eine Möglichkeit, die zunächst unbekannte Proportionalitätskonstante in seinem Gravitationsgesetz zu bestimmen. Doch dafür benötigte er die – ebenfalls noch unbekannte – Masse der Erde.

Die Planeten unseres Sonnensystems – und ihre Massen

Um den fraglichen Wert zu erhalten, schätzte Newton zunächst die mittlere Dichte unseres Planeten ab – anhand der Dichte von Gestein. Da der Radius und damit das Volumen der Erde bekannt waren, ließ sich mit dem Schätzwert für die Dichte nämlich die Masse der Erde berechnen. Die mittlere Dichte dürfte etwa fünfmal größer sein als jene von Wasser, nahm Newton an und kam so auf eine Erdmasse von etwa 5,5 × 10²⁴ Kilogramm. Mit Blick auf die recht grobe Schätzung kein schlechtes Ergebnis: Tatsächlich liegt der Wert nach heutigen Messungen bei 5,972 × 10²⁴ Kilogramm. Newton war damit in der Lage, die Größe der Proportionalitätskonstante im Gravitationsgesetz näherungsweise anzugeben.

Eine genauere Bestimmung dieser Gravitationskonstanten gelang erst 1797, als der britische Naturwissenschaftler Henry Cavendish eine „Gravitationswaage“ entwickelte. Damit ließ sich erstmals die gravitative Anziehungskraft zwischen kleinen Testkörpern direkt messen. Die Massen der Testkörper sind bekannt und so erlaubt das Experiment, aus der gemessenen Anziehungskraft die Proportionalitätskonstante im Gravitationsgesetz zu berechnen. Der exaktere Wert für die Gravitationskonstante und die viel leichter messbare Fallbeschleunigung erlaubten es nun, die Erdmasse mit weit höherer Genauigkeit als über das Volumen zu bestimmen. Die Erde war also der erste Planet, den die Naturwissenschaftler mithilfe des Newtonschen Gravitationsgesetzes wiegen konnten.

Vermessung des Sonnensystems

Knapp drei Jahrzehnte vor Cavendishs Experiment war es Forschern bereits gelungen, unser Sonnensystem zu skalieren. Zuvor waren zwar die Verhältnisse zwischen verschiedenen Entfernungen im Sonnensystem bekannt, jedoch keine absoluten Distanzen. Die Kenntnis sowohl der absoluten Entfernungen der Himmelskörper als auch der Gravitationskonstante ermöglichte es Astronomen schließlich, auch andere Planeten zu wiegen. Denn sieht man von anderen Kräften ab – die in der Himmelsmechanik nur eine sehr geringe Rolle spielen – bestimmt allein die Gravitation die Bahn eines Himmelskörpers.

Besonders einfach und anschaulich lässt sich dieser Zusammenhang am Beispiel eines Mondes darstellen, der einen Planeten umkreist. Die Anziehungskraft des Planeten hält den Mond auf seiner Bahn und lässt sich mithilfe des Newtonschen Gravitationsgesetzes beschreiben. Die Gravitationskraft wirkt hier als sogenannte Zentripetalkraft, da sie den Mond auf eine Kreisbahn zwingt. Dieser Umstand macht es möglich, die Masse des Planeten allein anhand von Bahnradius und Umlaufzeit des Mondes zu bestimmen [siehe Kasten]. Auf diese Weise konnten Astronomen außer Merkur und Venus – die keine Monde besitzen – alle Planeten im Sonnensystem wiegen. Um die Masse von Himmelskörpern zu messen, eignet sich sogar die Bahn von Raumsonden.

Waage für extrasolare Planeten

Etwas anders müssen Astronomen vorgehen, wenn sie Planeten bei anderen Sternen wiegen wollen. Hier macht man sich zunutze, dass streng genommen ein Planet nicht um seinen Zentralstern kreist, sondern beide um ihren gemeinsamen Schwerpunkt. Dadurch bewegt sich der Stern periodisch auf uns zu und wieder von uns weg. Die Bewegung ist zwar nur minimal, doch sie hinterlässt Spuren in seinem Lichtspektrum – hervorgerufen durch den sogenannten Dopplereffekt. Die charakteristischen Signaturen lassen sich nachweisen und messen. Und da sich ein Stern umso stärker bewegt, je größer die Masse des Planeten ist, können Wissenschaftler mit dieser Methode die Planetenmasse ermitteln.

Dafür muss aber nicht nur die Entfernung des Systems bekannt sein, sondern auch die Art des Sterns und damit dessen Masse. Beide Größen sind in der Astronomie zumeist aber gut zu bestimmen. In der Regel erhalten die Wissenschaftler trotzdem nur einen Mindestwert für die Masse. Denn solange sie die Orientierung der Planetenbahn im Raum nicht kennen, lässt sich der tatsächliche Abstand zwischen dem Stern und seinem Begleiter nicht genau beziffern. Nur wenn der Planet von der Erde aus regelmäßig vor seinem Stern vorüberzieht, ist diese Orientierung bekannt: Wir schauen direkt auf die Kante der Bahnebene. In diesem Fall zeigt die „Planetenwaage“ den Astronomen tatsächlich die Masse des Planeten an.