Quantenkryptografie – Sicherheit durch Quanteneffekte

Ob Briefwechsel, Telefongespräch oder E-Mail: Jeder Kommunikationsweg lässt sich anzapfen. Ziel der Kryptografie – der Wissenschaft vom Verschlüsseln – ist es, Spionen das Leben möglichst schwer zu machen. Moderne Verschlüsselungsverfahren arbeiten mit zufällig erzeugten Einmal-Schlüsseln. Doch auch der Austausch eines solchen Schlüssels kann abgehört werden. Abhilfe bieten Quanteneffekte: Hört ein Lauscher mit, so stört er die übertragene Information und wird dadurch entlarvt.
Das Thema Sicherheit spielt in unserem Leben eine immer größere Rolle – vom Schutz vor Terrorismus über die Sicherung der Energieversorgung bis zur Sicherheit im Straßenverkehr. Auch Informationen können wertvoll sein und müssen geschützt werden – nicht nur industrielle und militärische Geheimnisse, sondern auch beispielsweise die Zugangsdaten zu Bankkonten. Doch Schriftstücke können in die falschen Hände gelangen, Telefone abgehört und Internetverbindungen angezapft werden. In vielen Fällen hinterlässt der Spion keine Spur. Schlimm genug, wenn ein Geheimnis verraten wurde – doch noch schlimmer ist es, wenn wir keine Kenntnis von diesem Verrat haben.
Es ist deshalb kaum verwunderlich, dass die Wissenschaft des Verschlüsselns von Information, die so genannte Kryptografie, fast so alt ist wie die Menschheit selbst. Die Spartaner verwendeten im antiken Griechenland das Skytale-Verfahren, Julius Cäsar die Substitution und im zweiten Weltkrieg spielte die berühmte Enigma-Chiffriermaschine eine wichtige Rolle.
Moderne Kryptografiesysteme bestehen aus zwei Teilen, dem Schlüssel und dem Algorithmus. Der Algorithmus beschreibt, wie der Schlüssel auf die Ursprungsinformation angewendet werden muss. Bei einem Text könnte der Algorithmus beispielsweise der Austausch von Buchstaben sein und der Schlüssel würde dann angeben, welcher Buchstabe gegen welchen getauscht wird.
Eine informationstheoretisch „unknackbare“ Verschlüsselung erhält man dabei, wenn man einen zufällig erzeugten Schlüssel verwendet, der genau so lang ist wie die zu verschlüsselnde Information selbst (one time pad, Einmalverschlüsselung).
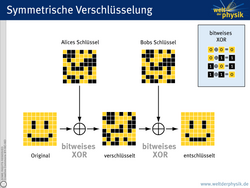
Man geht heute allgemein davon aus, dass der Spion das Verschlüsselungsverfahren, also den Algorithmus kennt. Die Sicherheit der Verschlüsselung basiert deshalb auf der Geheimhaltung des eingesetzten Schlüssels. Wenn es gelingt, einen identischen Schlüssel an zwei Kommunikationspartner, von nun an „Alice“ und „Bob“ genannt, zu verteilen, kann damit eine Nachricht sicher verschlüsselt und wieder entschlüsselt werden. Bei einer solchen „symmetrischen Schlüsselverteilung“ muss natürlich sichergestellt werden, dass der Schlüssel nicht in die Hände eines Spions fällt. Diesen möglichen Lauscher wollen wir von nun an „Eve“ nennen (von „eavesdrop“, engl. für belauschen).
Die Suche nach einem absolut sicheren Chiffrierverfahren reduziert sich damit auf die sichere symmetrische Schlüsselverteilung. Genau hier setzt die Quantenkryptografie, genauer: die Quantenschlüsselverteilung (engl. quantum key distribution) an: Sie bietet eine sichere Lösung für das Problem der Schlüsselverteilung.
Die Grundidee
Der wesentliche Unterschied der Quantenkryptografie gegenüber der klassischen Schlüsselverteilung liegt darin, dass die Information auf einzelnen Quantensystemen, den so genannten Qubits, kodiert ist. Als Träger werden dabei einzelne Photonen eingesetzt. Bei klassischen Übertragungsformen ist die Information dagegen in Pulsen aus vielen Photonen kodiert, wobei alle Photonen eines Pulses dieselbe Information tragen. So kann Eve einen Teil der Photonen des starken Pulses herausnehmen, um die Information auszulesen. Bei der Quantenkryptografie sitzt jedes Bit der Information auf einem einzelnen Photon. Diese Photonen kann Eve nun nicht einfach abzweigen, denn dann würden sie nie zu Bob gelangen und könnten nicht mehr Teil des Schlüssels werden.
Eve könnte stattdessen versuchen, das Photon zu messen und so an die Information zu gelangen. Doch hier macht ihr die Quantenphysik einen Strich durch die Rechnung. Denn die Quantengesetze erlauben es nicht, Messungen an Quantenzuständen durchzuführen, ohne diese zu beeinflussen. Dieselben Gesetze verbieten es Eve auch, eine identische Kopie des Photons zu erzeugen („No-Cloning-Theorem“) und die Messungen an dieser Kopie durchzuführen, um unentdeckt zu bleiben. Immer wenn Eve versucht, den Schlüssel abzuhören, ändert sie also zwangsläufig den Quantenzustand eines Qubits. Diese Änderungen tauchen als Fehler in der Übertragung zwischen Alice und Bob auf. Alice und Bob wissen somit, ob der Schlüssel abgehört wurde – und zwar noch bevor sie diesen für eine Chiffrierung der Nachricht einsetzen.
Das ist das Neue an der Quantenkryptografie: Sie ermöglicht eine sichere Schlüsselverteilung basierend auf quantenphysikalischen Gesetzen. Falls es zu einem Lauschangriff kommt, werden die Kommunikationspartner gewarnt und können den Schlüssel einfach verwerfen. Da nur ein Schlüssel abgehört wurde, ist die geheime Information selbst immer noch sicher.
Das BB84 Protokoll
Wie funktioniert die Quantenkryptografie im Detail? Um die Information auf einzelnen Photonen zu speichern, verwendet man häufig den Polarisationszustand, also die Richtung der Schwingungen des elektrischen Feldes des Photons.
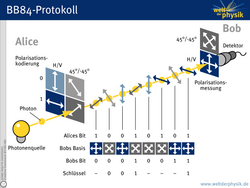
Alice kodiert dabei die klassischen Bit-Werte 0 und 1 des Schlüssels in Form bestimmter Polarisationszustände. Dabei dürfen nur orthogonale – also zueinander senkrecht stehende – Zustände zur Verwendung kommen, denn nur solche kann Bob mit einer Messung vollständig unterscheiden und so die Werte 0 und 1 wieder auslesen. Ein Paar solcher orthogonaler Zustände sind zum Beispiel die horizontale und vertikale Polarisation (H/V-Basis).
Alice kodiert also 0 als H und 1 als V und schickt diese Photonen zu Bob. Dieser kann in der H/V-Basis messen und erhält immer das gleiche Ergebnis der Polarisation und damit die von Alice kodierten Werte. Prinzipiell ließe sich so also ein identischer klassischer Bit-Schlüssel zwischen Alice und Bob austauschen. Doch diese Übertragung ist noch nicht abhörsicher. Eve könnte einfach eine Messung in der Basis H/V durchführen, die Polarisation bestimmen, danach ein Photon gleiche Polarisation erzeugen und weitersenden und somit die kodierte Information erhalten.
Um die Übermittlung des Schlüssels abhörsicher zu machen, muss Alice eine zweite, um 45 Grad gegenüber H/V gedrehte Basis verwenden. In dieser Basis +/- entsprechen 0 und 1 also einer Polarisation unter Winkeln von +45 und –45 Grad. Bei der Erzeugung des Schlüssels wählt Alice nun für jedes einzelne Bit des Schlüssels zufällig die Basis und sendet das so präparierte Photon an Bob.
Bei der Messung muss Bob jeweils zwischen den Basen H/V oder +/- wählen. In der Hälfte der Fälle misst Bob in der gleichen Basis, in der Alice die Information kodiert hat. In diesem Fall sind seine Ergebnisse korrekt und ein Bit für den Schlüssel kann gespeichert werden. In den anderen Fällen misst Bob in einer Basis, die nicht mit der von Alice gewählten übereinstimmt. Da ein horizontal präpariertes Photon zu gleicher Wahrscheinlichkeit bei +45 oder –45 Grad gemessen wird, gibt es in diesem Fall keine Korrelationen und das Photon kann nicht für den Schlüssel verwendet wird.
Um zu wissen, welche Photonen tatsächlich für den Schlüssel verwendet werden können, müssen sich Alice und Bob natürlich über ihre Basiswahl für jedes Photon austauschen. Dies kann – nach der Übertragung der Schlüsseldaten – sogar ganz öffentlich geschehen. Denn die Information über die Basis allein lässt keinen Rückschluss darauf zu, welcher Bit-Wert mit ihr kodiert wurde. Somit können Lauscher auch nichts über den geheimen Schlüssel erfahren, wenn sie nur den Basisvergleich mithören.
Lauschangriff!
Die Sicherheit dieses 1984 von Charles H. Bennett und Gilles Brassard entwickelten „BB84“- Protokolls beruht auf der Tatsache, dass die Regeln der Quantenphysik es Eve unmöglich machen, zu bestimmen, in welcher Basis (H/V oder +/–) Alice jeweils die einzelnen Photonen des Schlüssels kodiert hat. Eve weiß also nicht, in welcher Basis sie messen soll. Wählt sie zufällig die richtige Basis aus, so erhält sie tatsächlich die volle Information dieses Photons und bleibt auch unbemerkt. Wählt Eve aber falsch, so verändert ihre Messung den Polarisationszustand. Denn die Polarisation des Photons entspricht nach der Messung natürlich dem Messergebnis. Ein von Alice horizontal polarisiertes Photon wird durch Eves Messung in der +/- Basis auf +45 oder –45 Grad umpolarisiert. Da Bob aber ein in +/– Richtung polarisiertes Photon bei einer Messung in H/V mit gleicher Wahrscheinlichkeit in H oder V misst, erhält er in der Hälfte dieser Fälle ein falsches Ergebnis, das nicht mehr mit der von Alice gesendeten Information übereinstimmt. Ein Lauscher verursacht also Fehlern in der Übertragung.
Anhand dieser Fehler ist es nun möglich, zu bestimmen, ob ein Lauschangriff stattgefunden hat oder nicht. Dazu tauschen Alice und Bob einfach – wiederum durchaus öffentlich – eine Anzahl von Bits aus und schätzen daraus die Fehlerrate ab. Da es auch natürliche Übertragungsfehler geben kann, ist das Problem nun, einen Grenzwert zu finden, oberhalb dessen von einem Lauschangriff ausgegangen werden muss. Ein möglicher Lauscher könnte die technischen Fehler des Systems verwenden, um seinen Angriff zu tarnen. Deshalb müssen alle aufgetretenen Fehler immer einem Abhörer zugeschrieben werden. Um eine hohe Schlüsselrate zu erreichen, müssen also alle technischen Fehler auf ein Minimum reduziert werden.
Um eine „immerwährende Sicherheit“ zu gewährleisten, muss die stärkstmögliche Attacke angenommen werden. Dabei hat Eve alle Möglichkeiten, die innerhalb des Rahmens der Quantenmechanik erlaubt sind. Detektoren mit hundertprozentiger Effizienz und Quantenspeicher gehören dabei ebenso zu ihrem Werkzeug wie Quantencomputer. Trotzdem wird Eve Fehler hinterlassen, an denen man ihren Informationsgewinn ermessen kann. Für das BB84-Protokoll ergeben diese Überlegungen eine Grenze des Fehlers von elf Prozent. Liegt der Fehler darüber, so handelt es sich nicht mehr um eine sichere Übertragung. Ist der Fehler dagegen kleiner, so teilen Alice und Bob mehr Information als Eve mit Alice oder Bob. Mit einem speziellen Verfahren, der „privacy amlification“, lässt sich aus dem fehlerbelasteten unsicheren Schlüssel sogar Eves Information herauszufiltern und ein garantiert sicherer Schlüssel für Alice und Bob erstellen.
Verschränkung als Alternative
Im Jahr 1991 hat Artur Ekert ein alternatives Protokoll entwickelt, das auf der quantenmechanischen Verschränkung von Zuständen basiert. Dabei finden jeweils Paare von Photonen Verwendung, deren Polarisation durch ihren Entstehungsmechanismus zueinander parallel ist. Die Verschränkung führt dazu, dass bei der Messung der Polarisation in einer zufällig gewählten Basis die Polarisation des zweiten Photons augenblicklich einen Zustand in dergleichen Basis einnimmt.
Teilen Alice und Bob nun je ein Photon eines solchen verschränkten Paares, dann müssen ihre Messergebnisse immer identisch sein, wenn sie in derselben Basis messen. Damit ergibt sich – wie im Falle des BB84-Protokolls – ein Schlüssel. Statt der aktiven Kodierung wie bei BB84 führt Alice im E91-Protokoll eine passive Messung des Polarisationszustands durch.
Obwohl das E91-Protokoll sehr elegant ist, wird in der Praxis heute fast ausschließlich das BB84-Protokoll eingesetzt. Der Grund dafür ist, dass es für BB84 theoretisch fundierte Beweise für die Sicherheit des Verfahrens bei gegebenen Fehlern gibt. Beim E91-Protokoll dagegen sind die Zusammenhänge zwischen dem Lauschangriff und seinen Folgen für die übertragenen Daten noch nicht restlos geklärt.
Realisierung
Derzeit ist das größte Problem bei der technischen Realisierung von Quantenkryptografiesystemen die Messung einzelner Photonen. Die bislang erreichten Schlüsselraten sind eher bescheiden und liegen zumeist im Bereich von wenigen Kilobit pro Sekunde. Diese Rate ist auch durch die Länge des Übertragungswegs begrenzt. Im Gegensatz zu einem klassischen Puls aus vielen Photonen kann man einzelne Photonen wegen des No-Cloning-Theorems nicht durch einen Verstärker schicken. Verluste in der Übertragung wirken sich deshalb direkt auf den Schlüssel aus: Der Verlust eines Photons bedeutet den Verlust eines Bits.
Die heute in Labors getesteten Systeme kommen dennoch auf über hundert Kilometer Übertragungslänge in Glasfasern mit Schlüsselraten um hundert Bit pro Sekunde. Kürzere Strecken, wie sie in innerstädtischen Glasfaser-Netzwerken auftreten, können mit zehn Kilobit pro Sekunde versorgt werden.
Wenn die Photonen nicht durch Glasfasern, sondern per Teleskop durch die Luft übertragen werden, verringert sich die Dämpfung und es lassen sich längere Strecken überbrücken. So konnte in Experimenten eine Quantenkryptografieverbindung über 144 Kilometer zwischen den kanarischen Inseln Teneriffa und La Palma realisiert werden.
Für einen Einsatz in der Praxis sind aber nicht nur die überbrückbare Entfernung und die Übertragungsrate von Bedeutung. Wichtig ist auch, dass die Systeme ausfallsicher und leicht zu bedienen sind. In den letzten Jahren gelang tatsächlich der Sprung von raumfüllenden Laboraufbauten zu kompakten und zuverlässigen Geräten. Spin-off-Firmen diverser Universitätsgruppen haben bereits damit begonnen, ihre Systeme externen Kunden anzubieten. Die Quantenkryptografie ist damit die erste kommerziell einsetzbare Anwendung der zwar fundamentalen, aber nicht immer intuitiven Gesetze der Quantenphysik.
Quelle: https://www.weltderphysik.de/gebiet/technik/quantenmechanik-quantentechnik/quanten-kryptographie/