Topologische Materiezustände

David Thouless, Duncan Haldane und Michael Kosterlitz erhalten 2016 den Physiknobelpreis „für die theoretische Entdeckung von topologischen Phasenübergängen und topologischen Phasen der Materie”. Frank Pollmann vom Max-Planck-Institut für Physik komplexer Systeme in Dresden erklärte im Podcast, woran die drei Nobelpreisträger geforscht haben, was topologische Phasen sind und welche Relevanz sie in der modernen Festkörperphysik haben.

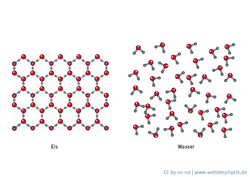
Auf den ersten Blick könnten Eis, Wasser und Dampf völlig unterschiedliche Stoffe sein – erst auf mikroskopischer Ebene wird klar, dass sich Feststoff, Flüssigkeit und Gas aus dem gleichen Molekül – nämlich H₂O – zusammensetzen.

Frank Pollmann vom Max-Planck-Institut für Physik komplexer Systeme

Frank Pollmann: „Und diese einzelnen Teilchen oder diese Moleküle wechselwirken miteinander und spüren sich gegenseitig. Im flüssigen oder im gasförmigen Wasser sind die Wassermoleküle ungeordnet, dass heißt, diese Wassermoleküle haben keine bevorzugte Position relativ zueinander und auch die Orientierung der Wassermoleküle ist beliebig. Wenn man das Wasser jetzt allerdings abkühlt, es also unter null Grad Celsius bringt, dann formen die Wassermoleküle Kristallstrukturen, um die Energie zu minimieren.“

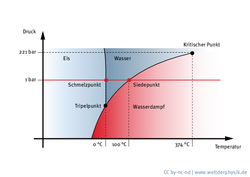
Durch die periodische Anordnung der Moleküle im Kristallgitter ändern sich die mechanischen Eigenschaften drastisch – und so kann man in Wasser schwimmen und auf Eis laufen. Bei welcher Temperatur und welchem Druck sich ein Stoff im festen, flüssigen oder gasförmigen Zustand befindet, halten Physiker in sogenannten Phasendiagrammen fest.

„In einem Phasendiagramm schaut man sich an, wie sich ein System als Funktion von gewissen Parametern verhält. Bei Wasser etwa beobachten wir, welche Phasen auftreten, wenn man beispielsweise die Temperatur ändert. Diese Phasendiagramme helfen uns, verschiedene Phasen der Materie zu klassifizieren. Insbesondere treten zwischen verschiedenen Phasen Phasenübergänge auf, die durch gewisse Unstetigkeiten gekennzeichnet sind. Beim Wasser ändert sich beispielsweise das Volumen schlagartig, wenn man von der flüssigen zur gasförmigen oder von der flüssigen zur festen Phase übergeht.“

Phasendiagramm von Wasser

Für Physiker ist nun interessant, ob man in einem solchen Diagramm vielleicht einen Pfad finden kann, der zwei Aggregatzustände miteinander verbindet, ohne dabei einen Phasenübergang zu durchlaufen. Entlang eines solchen Pfades würde sich also keine Eigenschaft des Systems – wie das Volumen beim Wasser – sprunghaft verändern.

„Das Ganze lässt sich wieder gut am Beispiel des Wassers illustrieren. Wenn man in der Küche das Wasser erhitzt, dann stellt man fest, dass es einen Phasenübergang zwischen dem flüssigen und dem gasförmigen Wasser gibt – das Wasser fängt bei circa hundert Grad an zu kochen. Tatsächlich kann man jedoch einen anderen Pfad wählen: Wir können das Wasser unter hohem Druck erhitzen und dann stellen wir fest, dass es einen Pfad gibt, der das Wasser von der flüssigen in die gasförmige Phase umformt, ohne dass ein Phasenübergang auftritt.“

Oberhalb eines bestimmten Druckes und einer bestimmten Temperatur lassen sich flüssiges Wasser und Wasserdampf daher nicht mehr unterscheiden. Sie liegen in ein und derselben Phase. Im Gegensatz dazu zeigt sich, dass Wassereis abhängig von Temperatur und Druck mehrere Phasen besitzt. Um die verschiedenen Phasen eines System eindeutig zu identifizieren, müsste man genaugenommen also alle möglichen Parameter – Temperatur, Druck, Magnetfelder und so weiter – variieren und nachsehen, ob Phasenübergänge auftreten. Das ist natürlich nicht umsetzbar.

„Also brauchen wir ein formales Prinzip, um verschiedene Phasen der Materie klassifizieren zu können. Ein solches Prinzip wurde 1937 von Lev Landau hergeleitet. Es besagt, dass zwei Zustände in derselben Phase sind, wenn sie die gleichen Symmetrien haben.“

Eis und flüssiges Wasser

Sowohl im flüssigen Wasser als auch im Wasserdampf schwirren die Moleküle ungeordnet umher und sind relativ gleichmäßig im Raum verteilt. Auf mikroskopischer Ebene fiele es daher schwer, sich zu orientieren – denn egal um welche Strecke man sich bewegt oder um welchen Winkel man sich dreht, alles sehe gleich aus. Physiker sprechen von kontinuierlicher Translations- beziehungsweise Rotationssymmetrie. Im Wassereis sind die Moleküle dagegen regelmäßig in einem Kristallgitter angeordnet – und die Aussicht würde sich unterscheiden, je nachdem an welcher Position innerhalb des Gitters man sich befindet und in welche Richtung man schaut. Die kontinuierliche Translations- und Rotationssymmetrie, die flüssiges Wasser und Wasserdampf aufweisen, sind damit gebrochen.

„Eine Konsequenz dieser Symmetriebrechung ist, dass wir diese Phasen mithilfe sogenannter lokaler Ordnungsparameter unterscheiden können. Das heißt, wir können eine lokale Messung an dem System machen und dann entscheiden, ob diese Symmetrien gebrochen sind oder nicht.“

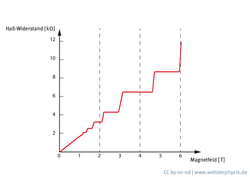
Diese Methode lässt sich auf eine Vielzahl von physikalischen Systemen anwenden – und so etwa Kristalle von Flüssigkeiten unterscheiden, aber beispielsweise auch Magnete von nichtmagnetischen Systemen oder gewöhnliche elektrische Leiter von Supraleitern. Doch mit dem Quanten-Hall-Effekt entdeckte Klaus von Klitzing in den frühen 1980er-Jahren eine komplett neue Phase der Materie: Der Physiker ließ bei tiefen Temperaturen Strom durch ein extrem dünnes, nahezu zweidimensionales Material in einem Magnetfeld fließen, wodurch sich senkrecht zur Flussrichtung eine elektrische Spannung aufbaute. Überraschenderweise wuchs diese sogenannte Hall-Spannung nicht kontinuierlich mit dem äußeren Magnetfeld an, sondern stufenweise.

Quanten-Hall-Effekt

„An den Stufen formt das System einen isolierenden Zustand, also einen Isolator. Alle diese Isolatoren an den verschiedenen Stufen stellen verschiedene Phasen der Materie dar. Das können wir erneut mit dem Wassereis vergleichen: Dort haben wir die Temperatur als einen Parameter gehabt und gesehen, wie wir beispielsweise von der Eisphase in die flüssige Phase übergegangen sind. Hier hingegen gehen wir jetzt als Funktion vom Magnetfeld durch verschiedene Phasen hindurch.“

Doch anders als beim Wasser unterscheiden sich die verschiedenen Phasen beim Quanten-Hall-Effekt nicht bezüglich ihrer Symmetrie – eine lokale Messung der Eigenschaften gibt also keinen Aufschluss darüber, ob zwei Zustände des Systems in einer Phase liegen oder nicht. Einen alternativen Weg, um auch solche ungewöhnlichen Phasen zu charakterisieren, fanden David Thouless, Duncan Haldane und Michael Kosterlitz. Die drei Physiker griffen dafür auf das mathematische Konzept der Topologie zurück.

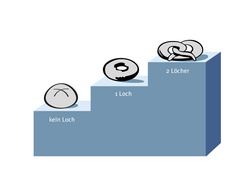
„Topologie ist ein Feld der Mathematik, das sich mit Größen auseinandersetzt, die nicht durch stetige Umformungen verändert werden können. Das vermutlich bekannteste Beispiel dafür ist der Unterschied zwischen einem Torus und einer Kugel. Diese beiden Formen können nicht durch Kneten ineinander umgeformt werden – es sei denn, man schneidet sie auf und klebt sie neu zusammen. Mathematisch unterscheiden sich diese beiden durch sogenannte topologische Invarianten. In dem Fall ist das der sogenannte Genus – oder die Anzahl der Löcher –, der bei der Kugel null und bei dem Torus eins beträgt.“

Topologie am Beispiel von Backwaren

Mithilfe dieser topologischen Eigenschaften lassen sich Objekte klassifizieren – ein Brötchen und eine Kugel wären demnach in einer Klasse, ein Bagel und ein Torus in einer anderen. Bei einer Brezel ist der Fall schon nicht mehr so klar, denn je nach Vorliebe des Bäckers hat diese mal zwei oder auch drei Löcher. Doch die Mathematik hat auch hier eine Lösung: Denn die topologische Invariante lässt sich eindeutig berechnen, mithilfe des Satzes von Gauß-Bonnet.

„Dieser besagt, dass wir, wenn wir über die gesamte Krümmung der Fläche integrieren beziehungsweise sie aufsummieren, eine Zahl erhalten, die nur vom Genus – oder der Anzahl der Löcher – abhängt. Das heißt, wir nehmen jetzt eine Kugel, integrieren oder summieren über die gesamte Krümmung und erhalten die Zahl. Jetzt nehmen wir diese Kugel und kneten sie – wir ändern also lokal die Krümmung. Die Zahl aber, die sich aus der Summierung der ganzen Krümmung ergibt, bleibt dabei unverändert.“

Dadurch lassen sich Objekte – unabhängig von ihren lokalen Eigenschaften – eindeutig einer Klasse zuordnen. Diesen Ansatz übertrugen Thouless und seine Kollegen auf den Quanten-Hall-Effekt: Die Physiker schauten sich dazu das quantenmechanische Verhalten der Elektronen im Experiment an, das sich mithilfe von Wellenfunktionen beschreiben lässt. Aus der Gesamtheit dieser quantenmechanischen Wellenfunktionen lässt sich eine Größe – analog zur Krümmung der Kugel – ableiten, aus der man ebenfalls eine für jede Phase charakteristischen Wert – eine topologische Invariante – berechnen kann. Dadurch verknüpften die Physiker um Thouless die stufenweise ansteigende Hall-Spannung direkt mit der Topologie des Quanten-Hall-Zustandes.

„Der gefundene Zusammenhang zwischen der Hall-Spannung und der topologischen Invariante erklärt auch, warum die Hall-Spannung so präzise quantisiert ist – also die Hall-Spannung kann mit einer Genauigkeit von 1 zu 10¹⁰ bestimmt werden. Das ist eine sehr faszinierende Eigenschaft, weil im Festkörper natürlich lokale Verunreinigungen und Störstellen sind, die diese topologische Invariante aber eben nicht beeinflussen.“

Spinkette

Das Prinzip ist dasselbe wie bei einer Kugel, bei der die Summe aller Krümmungen – beziehungsweise die topologische Invariante – unverändert bleibt, auch wenn man sie lokal verformt. Im Lauf der Zeit stellte sich heraus, dass sich der Ansatz auch bei weiteren untypischen physikalischen Systemen bewährte, wie etwa den von Duncan Haldene untersuchten Spinketten. Auf diesen eindimensionalen Ketten sind magnetische Momente ähnlich winzigen Kompassnadeln aufgereiht und wechselwirken miteinander. Haldane fand 1987 heraus, dass sich eine spezielle Form dieser Ketten anders verhält als bis dahin vermutet.


„Und damit hat er den Grundstein für spätere Arbeiten gelegt, die gezeigt haben, dass diese Phasen ebenfalls durch topologische Invarianten beschrieben werden können.“

Ein weiteres Beispiel sind die bereits in den 1970er-Jahren von Michael Kosterlitz und David Thouless untersuchten zweidimensionalen Spinsysteme, die man sich wie ein regelmäßiges Gitter aus Kompassnadeln vorstellen kann.

„Bei diesen Systemen tritt bei endlichen Temperaturen keine Ordnung auf. Deshalb war man davon ausgegangen, dass es dort auch keine Phasenübergänge geben würde. Die Entdeckung von Kosterlitz und Thouless war daher eine Überraschung: Sie konnten zeigen, dass es in diesen Systemen doch Phasenübergänge gibt. Und diese Phasenübergänge können verstanden werden, indem man Phasen hat, in denen Anregungen in Form von Wirbeln entweder gebunden sind oder frei.“

Thouless, Haldane und Kosterlitz

Auch hier spielen topologische Eigenschaften wieder die entscheidende Rolle. Mit dem von Kosterlitz und Thouless entwickelten Modell eines topologischen Phasenübergangs in zwei Dimensionen ließen sich später unter anderem Experimente mit dünnen Schichten aus supraflüssigem Helium oder aus verschiedenen supraleitenden Materialien erklären. Mit ihren Arbeiten haben Thouless, Haldane und Kosterlitz wichtige theoretische Beiträge zur Physik geleistet und gelten als Pioniere in ihrem Forschungsgebiet – 2016 erhielten sie dafür den Nobelpreis für Physik. Topologische Phasen haben aber auch praktische Seiten – die enorm präzise Quantisierung der Hall-Spannung machen sich Physiker bereits zunutze.

„So wird die Einheit des elektrischen Widerstandes über den Hall-Effekt definiert und es wird auch diskutiert, die Einheit der Masse über den Hall-Effekt – zusammen mit einem anderen physikalischen Effekt – zu definieren.“

Derzeit ist die Einheit der Masse, das Kilogramm, noch über das Urkilogramm definiert – einen kleinen Metallzylinder aus Platin und Iridium. Für 2018 ist eine Neudefinition geplant, ob über die Wattwaage, die den Quanten-Hall-Effekt ausnutzt, oder das sogenannte Avogadroprojekt, bei dem eine Siliziumkugel als Referenzobjekt dient, ist noch unklar. Eine andere mögliche Anwendung topologischer Phasen sehen Physiker in Quantencomputern. Anders als klassische Rechner funktionieren diese Computer nach quantenmechanischen Prinzipien, wodurch sie bestimmte Aufgaben – etwa das Durchsuchen großer Datenbanken – sehr viel schneller erledigen könnten.

Wattwaage NIST-4

„Ein Problem bei den Quantencomputern ist, dass die Quanteninformationen sehr flüchtig sind und durch lokale Störungen – wie beispielsweise ein Photon, das eintrifft – zerstört werden können. Der Physiker Alexei Kitajew hat vorgeschlagen, topologische Systeme zu verwenden, um Quanteninformation zu speichern. Und der Vorteil am Speichern der Quanteninformation in topologischen Systemen ist wiederum, dass die Informationen nicht durch lokale Störungen zerstört werden können.“

Ein solcher topologischer Quantencomputer wäre damit deutlich robuster als die derzeit verfolgten Ansätze, in denen die Quanteninformation beispielsweise in ultrakalten Ionen oder supraleitenden Bauelementen gespeichert wird. Während für solche „herkömmlichen“ Quantencomputer schon erste Prototypen existieren, handelt es sich bei den topologischen Systemen bisher nur um eine spannende Idee. Erst einmal müssen Physiker passende Materialien finden, in denen entsprechende topologische Phasen realisiert werden können. Aussichtsreiche Kandidaten sind beispielsweise sogenannte Quantenspinflüssigkeiten oder topologische Supraleiter.

„Die Tatsache, dass sich topologische Phasen nicht durch Symmetriebrechung charakterisieren lassen, macht es sehr schwer, diese Phasen experimentell zu bestimmen. Und daher wird gerade aktiv daran gearbeitet, Vorhersagen zu machen, die experimentell überprüft werden können.“

Mithilfe der theoretischen Vorgaben ließe sich dann gezielt nach Materialien suchen – und beispielsweise durch Neutronenstreuung herausfinden, ob diese tatsächlich die gewünschten Eigenschaften besitzen. Idealerweise sollten diese Materialien die topologischen Phasen natürlich bei Raumtemperatur und ohne starke Felder zeigen – also anders als beim Quanten-Hall-Effekt. Bislang sind die Theoretiker aber noch am rechnen – und die experimentelle Erforschung dieser Phasen steht noch am Anfang.