Flugbahn – die Rolle des Luftwiderstands

Schüsse aus großer Distanz sind durchaus zu halten, wenn der Torwart die Flugbahn des Balls gut einschätzen kann. Je länger der Ball in der Luft ist, desto einfacher sollte dies sein. Die Einflüsse des Luftwiderstandes, des Windes und eines möglichen Dralls auf die Flugkurve müssen dabei berücksichtigt werden. Wie wichtig sind dabei die einzelnen Komponenten?

Flugbahn eines Fußballs mit Luftwiderstand

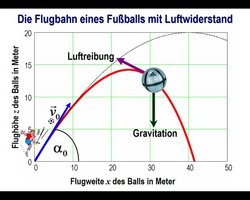
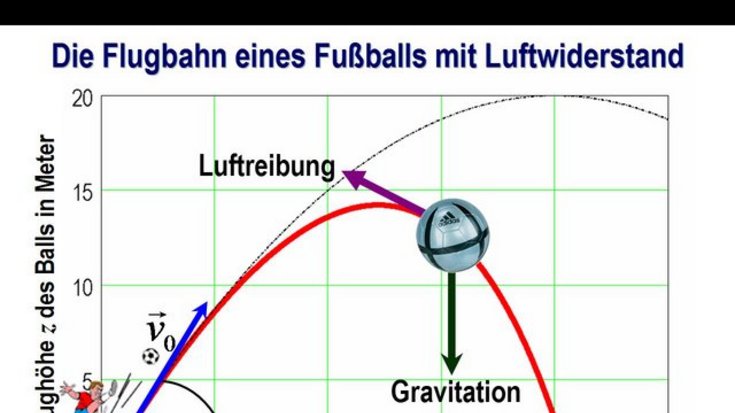
Die obige Grafik zeigt die Flugbahn eines Fußballs und die Kräfte, die auf ihn einwirken. Nach rechts, in x-Richtung, und nach oben, in z-Richtung, sind die jeweilige Flugweite und Flughöhe des Balls aufgetragen. Die rote Linie gibt dann die Flugkurve des Balls wieder. Jeder Punkt auf dieser roten Linie gehört zu einer bestimmten Flugweite und Flughöhe. Damit wird Lage des Balls im Raum eindeutig angegeben. Die Skalen in x- und z-Richtung sind unterschiedlich, so dass die Kurve stärker nach oben „auseinander gezogen“ erscheint. In Wirklichkeit verläuft die Flugkurve des Balls daher deutlich flacher. Bei der Berechnung der Flugkurve kommt es auf mehrere Parameter an. Die gezeigte Kurve ist für eine Abschussgeschwindigkeit von v₀ = 100 km/h und einen Abschusswinkel von ⍺₀  = 45° berechnet worden. Diese Werte entsprechen etwa denen eines Abstoßes von einem Torwart im Profifußball. Wichtig ist nun aber, dass der Luftwiderstand mit berücksichtigt wurde.

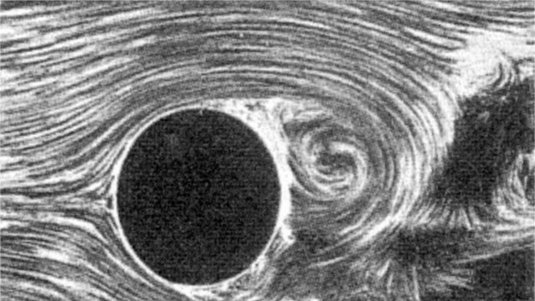
Auf den Ball wirken während des Fluges durch die Luft die verschiedensten Kräfte ein, von denen wir im ersten Teil der Untersuchung nur die immer senkrecht nach unten zeigende Erdanziehungskraft berücksichtigt haben. Jeder Gegenstand wird auf der Erde mit der konstanten Erdbeschleunigung von g = 9.81 m/s² zum Erdmittelpunkt hin beschleunigt und somit angezogen. Die Erdbeschleunigung ist dabei unabhängig von der Masse des Körpers, obwohl man das Gefühl hat, dass schwerere Körper schneller fallen als leichte. Dies liegt aber am Luftwiderstand, den wir nun mit berücksichtigen wollen und der einen großen Einfluss auf die Flugkurve eines Fußballs hat. Der Luftwiderstand übt eine zusätzliche Kraft auf den Fußball aus, die parallel und entgegengesetzt zur augenblicklichen Bewegungsrichtung gerichtet ist, wie in der Abbildung vorher angedeutet.

Ballistische Kurve

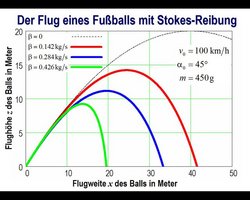
Bei der Berechnung wurde eine Reibungskraft zugrunde gelegt, die linear mit der Geschwindigkeit des Fußballs ansteigt. Man bezeichnet diesen Fall als „Stokes-Reibung“. Es gilt also F_Luftreibung = β · v. Die rote Kurve in der vorherigen Grafik zeigt dann die Flugkurve eines Fußballs für den Fall β = 0,142 kg/s. Dieser empirische Wert hängt direkt mit der Beschaffenheit der Oberfläche eines Fußballs zusammen. Man beachte nun, dass die Flugkurve mit Luftwiderstand (rote durchgezogene Linie) sich drastisch verändert hat, wenn man sie mit der Kurve ohne Luftwiderstand (gestrichelte schwarze Linie) vergleicht. Ohne Luftwiderstand käme der mit 100 km/h unter einem Abschusswinkel von 45 Grad getretene Ball etwa 80 Meter weit, würde etwa 20 Meter hoch steigen und ergäbe eine völlig symmetrische Flugkurve, die auch als „Wurfparabel“ bezeichnet wird.

Die analytische Berechnung der Schußhöhe

Unter Berücksichtigung des Luftwiderstandes fliegt der unter denselben Anfangsbedingungen getretene Ball nur etwa 42 Meter weit, fliegt nur 14 Meter hoch und die Flugkurve ist nun stark asymmetrisch. Es handelt sich um eine so genannte „ballistische Kurve“, bei der der Ball – nachdem er die maximale Höhe erreicht hat – in der zweiten Flugphase nicht mehr so weit kommt wie in der ersten. In unserem in der Abbildung gezeigten Beispiel erreicht der Ball nach etwa 24 Metern Flugweite seine maximale Höhe und fliegt dann aber nur noch weitere 18 Meter weit bis er auf dem Boden ankommt. 42 Meter sind übrigens eine durchaus realistische Abschussweite für einen Abstoß eines Torwartes, da dies in etwa die Distanz vom Fünf-Meter-Raum bis kurz hinter den Mittelkreis ist.

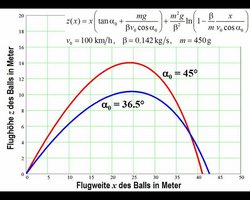
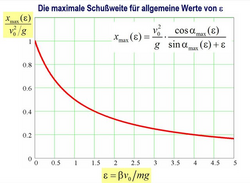
Mathematisch kann man die Flugkurve z(x) eines Fußballs unter Berücksichtigung des Luftwiderstandes F_Luftreibung = β · v durch eine recht komplizierte Formel ausdrücken. Dies und die analytische Berechnung der Schusshöhe ist für Experten einmal in der nebenstehenden Abbildung zusammengestellt.

Den Einfluss des Reibungsparameters β zeigt die folgende Abbildung. Man erkennt, dass eine Vergrößerung von β die Flugkurve drastisch im zweiten Abschnitt verändert.

Der Flug eines Fußballs mit Stokes-Reibung

Der optimale Schusswinkel für die maximale Flugweite eines Fußballs ist nicht mehr ⍺₀  = 45° wie bei der idealisierten Flugbahn, wenn der Luftwiderstand mit berücksichtigt wird. Qualitativ kann die Frage, ob der optimale Abschusswinkel dann größer oder kleiner als 45 Grad ist, sofort beantwortet werden: Er muss abnehmen. Generell gilt, dass je länger die Luftreibungskraft wirkt, desto mehr Bewegungsenergie wird dem Ball entzogen und desto kürzer wird er daher fliegen. Bei Abschusswinkeln über 45 Grad ist der Ball aber deutlich länger in der Luft als bei solchen unter 45 Grad. Also sollte der optimale Abschusswinkel sinken. Dies aber konkret auszurechnen ist nicht ganz einfach und gelingt nur in Spezialfällen. Für unseren Fall zeigt die nebenstehende Abbildung das Ergebnis einer numerischen Analyse.

Das Ergebnis einer numerischen Analyse

Der optimale Abschusswinkel ist also auf 36,5 Grad gesunken. Der Ball fliegt dann zwar nicht mehr so hoch wie der unter 45 Grad abgeschossene, aber er fliegt etwa 1,50 Meter weiter – kein großer Gewinn, aber immerhin. Generell gilt daher, dass ein Torhüter beim Abstoß etwa das „Fenster“ 30 < ⍺₀ < 45° einhalten sollte, um annähernd die optimale Flugweite zu erzielen. Ansonsten ist der Ball zu flach (⍺₀ < 30°) oder es geht zuviel Energie in die Flughöhe (⍺₀ > 45°) des Balls.

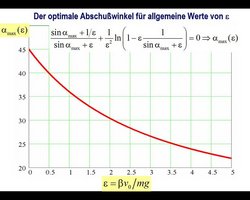
Eine aufwendige allgemeine Analyse ergibt, dass der optimale Abschusswinkel von einem Parameter ε abhängt, der folgendermaßen von der Abschussgeschwindigkeit v₀, dem Ballparameter β, der Masse des Fußballs und der Erdbeschleunigung g abhängt: $$ \epsilon = \frac{\beta \cdot v_0}{m \cdot g}. $$ Anschaulich ist dies das Verhältnis zwischen dem Luftwiderstand (β · v₀) und der Gravitation (m · g), also der Größe der beiden Kräfte, die auf den Fußball während des Fluges durch die Luft einwirken. Für den optimalen Abschusswinkel als Funktion dieses Parameters ε ergibt sich dann der in der nebenstehenden Abbildung gezeigte Zusammenhang.

Der optimale Abschusswinkel

Für Experten sei angemerkt, dass sich der optimale Abschusswinkel als Lösung der transzendenten Gleichung, die oben in der Grafik zu sehen ist, ergibt. Für ε = 1, also wenn die Luftreibung genauso groß ist wie die Gravitation, hat diese Gleichung sogar eine exakte analytische Lösung von ⍺₀ = 35,6°.

Mit einer Abschussgeschwindigkeit v₀ = 100 km/h und dem Ballparameter β = 0,142 kg/s ergibt sich für unseren Beispielschuss, den wir bisher immer betrachtet haben, ein Wert des Parameters ε von 0,89, wobei eine Ballmasse von m = 450 g verwendet wurde. Aus der Grafik lesen wir dann einen optimalen Abschusswinkel von etwa 36,5° ab, also den Wert, den wir bereits kennen. Für die halbe Abschussgeschwindigkeit v₀ = 50 km/h ergibt sich ε = 0,45. aus der Grafik liest man dann ⍺₀ = 40° als den Abschusswinkel ab, der die größte Flugweite des Balls ergibt.

Zum Abschluss soll in der folgenden Grafik noch gezeigt werden, wie die maximale Schussweite, also die bei gegebener Abschussgeschwindigkeit für den optimalen Abschusswinkel erzielte Flugweite eines Fußballs, vom Luftwiderstand abhängt. Ohne Luftwiderstand wäre diese Flugweite einfach gegeben durch v₀²/g, was für v₀ = 100 km/h und g = 9,81 m/s² eine Flugweite von etwa 80 Metern ergibt. Die Abbildung zeigt nun die jeweilige Flugweite bezogen auf diesen Wert ohne Luftwiderstand.

Die maximale Schussweite

Wir lesen ab, dass sich für ε = 0,89, was unserem Beispielschuss entspricht, der Wert von etwa 0,5 ergibt. Das bedeutet, dass sich die Schussweite durch den Luftwiderstand halbiert, so wie wir das bisher auch immer gesehen haben. Im Fall der halben Abschussgeschwindigkeit von v₀ = 50 km/h lesen wir für den Wert ε = 0,45 aus der Grafik den Wert 0,7 ab. Der Luftwiderstand reduziert dann die maximale Schussweite also nur auf 70 Prozent ihres Wertes ohne Luftwiderstand.

Kanonenkugeln sind einfacher zu berechnen

Aber alles, was wir hier für den Flug eines Fußballs besprochen haben, gilt auch für den Flug einer Kanonenkugel. Deswegen haben wir im Prinzip „Ballistik“ betrieben und uns auch den Methoden dieser schon lange bekannten Disziplin bedient. Menschen haben sich schon immer für das Flugverhalten von Kanonenkugeln interessiert und haben versucht deren Flugverhalten genauestens zu berechen. Allerdings ist für eine etwa 100 kg schwere Kanonenkugel der Parameter 0 deutlich kleiner als für einen Fußball, selbst wenn man bedenke, dass eine Kanonenkugel in der Regel schneller durch die Luft fliegt. Dies machte die Berechnungen für Kanonenkugeln leider viel einfacher, so dass sie auch schon vor etwa 300 Jahren ohne Computer durchgeführt werden konnten. Fußbälle hingegen bewegen sich aber immer im Bereich 0 &asymp, 1, ein Bereich der nicht ohne Computer analysiert werden kann. Vor etwa 300 Jahren hätte man also schon mit unseren Fußbällen spielen können - ihre Flugbahnen waren aber nicht vorauszuberechnen!

Torhüter haben aber keine Zeit für eine Computeranalyse. Allerdings verstehen wir nun, dass dieses Unterschätzen durchaus vorkommen kann, da die „ballistischen Flugkurven“ von Fußbällen sehr asymmetrisch und damit nicht leicht vorhersehbar sind.

Sie haben wieder einmal gesehen, dass Fußball manchmal recht kompliziert sein kann. Wieder haben wir nur den „einfachen“ Flug eines Fußballs durch die Luft betrachtet und sind schon auf recht komplexe Zusammenhänge gestoßen. Dabei habe ich Ihnen immer noch nicht alles erzählt und wir haben zum Teil drastische Vereinfachungen vorgenommen. Weiter geht es im dritten Teil der Fußballflugbahn.