„Es kommt auf die Formänderung an“
Franziska Konitzer
Ob Vögel in der Luft, Fische im Wasser oder Mikroorganismen im Körper – sie alle verlassen sich mehr oder weniger auf die gleichen Mechanismen, um sich fortzubewegen. Mithilfe vereinfachter Modelle versuchen Wissenschaftler diesen Abläufen auf die Spur zu kommen. Ubbo Felderhof von der RTWH Aachen geht dabei nun einen Schritt weiter: In seinem Modell berücksichtigt er nicht wie bisher nur die Reibung, sondern auch die Trägheit von Mikroorganismen, indem er sie als kleine Kügelchen in einer Flüssigkeit darstellt. Wir sprachen mit dem Forscher über die im Fachmagazin „Physics of Fluids“ vorgestellten Ergebnisse.
Welt der Physik: In ihrem Modell stellen Sie schwimmende Mikroorganismen vereinfacht als kleine Kugeln dar. Wie genau beschreiben die Ergebnisse die tatsächlichen Abläufe?
Ubbo Felderhof: Das Modell ist nicht dazu da, die Wirklichkeit gut darzustellen. Man kann aber einen Anfang machen, weil sich mit solchen Kugeln relativ leicht rechnen lässt: Wir wissen, wie eine Kugel mit einer Flüssigkeit wie Wasser wechselwirkt und wie die Strömungsfelder aussehen. Das Problem dabei ist, dass man für jedes der Kügelchen ein eigenes Strömungsfeld hat, die sich alle überlagern. Das sind also komplizierte Felder, die im Endeffekt eine Schwimmbewegung verursachen. Für kompliziertere Formen ist das einfach zu schwierig zu berechnen.
Wie kommt eine Schwimmbewegung zustande?
Die vorherrschende Erklärung für Schwimmen und auch für Fliegen ist, dass man einen Schub, einen Auftrieb, braucht, um einen Körper zu bewegen. Demnach wäre dieser Schub nötig, um den Strömungswiderstand zu überwinden. Aber das ist dem Modell zufolge nicht ganz richtig: Denn wenn man diese Kräfte über die Zeit mittelt, findet man heraus, dass der Schub gleich null ist – und der Strömungswiderstand auch. Es stimmt demnach zwar, dass beide gleich groß sind, im Durchschnitt sind aber eben beide null.
Was verursacht dann die Bewegung?
Im Modell schwingen die Kügelchen entlang einer Achse. Das ist eine periodische Bewegung, so wie sie auch von tatsächlichen Mikroorganismen ausgeführt wird. Diese innere Bewegung des Körpers bewirkt, dass sich auch die Position seines Masseschwerpunkts systematisch ändert. Sie wirkt letztendlich wie ein Schub, ist aber nicht dasselbe. Ich nenne das „Impetus“, um da keine Verwirrung zu stiften.
Also wenn ich keine schwingenden Kügelchen hätte, sondern einen starren Körper, könnte sich dieser nicht fortbewegen?
Doch, das geht schon, solange man Oberflächenwellen auf dem Körper laufen lässt. Es kommt auf die Formänderung an.
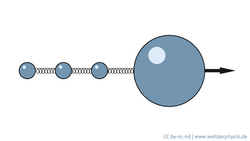
Sie haben in ihrem Modell auch eine größere Kugel hinzufügt. Was hatte das für Folgen?
Ich habe jetzt also drei kleine Kügelchen, die eine große, starre Kugel fortbewegen müssen. So etwas kommt auch oft in der Natur vor, wenn ein Organismus einen großen Kopf oder einen großen Körper hat, und kleine Anhängsel, die die eigentliche Bewegung verursachen. Das wollte ich modellieren und habe herausgefunden, dass das im Prinzip gar nicht so viel ändert. Als Kräfte spielen die Reibung zwischen den Kügelchen und der Flüssigkeit eine Rolle sowie die Trägheit. Die Bedingung dabei ist zwar, dass auf die große Kugel keine Kraft wirkt, aufgrund der Relativbewegung der Kugeln untereinander gibt es trotzdem eine Nettobewegung und der gesamte Organismus kann schwimmen.
Wie kann man das Modell noch weiter verbessern?
Wenn die Körper größer werden oder wenn eine Kugel mit hoher Geschwindigkeit regelrecht durch eine Flüssigkeit schießt, bekommt man Wirbel. Bei langsamen Bewegungen sind die Strömungsfelder relativ einfach. Wirbel aber machen die Sache viel komplizierter, man muss sie aber für größere Körper immer berücksichtigen. Das versuche ich jetzt zu modellieren.
Quelle: https://www.weltderphysik.de/gebiet/materie/nachrichten/2017/es-kommt-auf-die-formaenderung-an/