Wie entstehen Pandemien?

Globale Epidemien – Pandemien – werden erst durch die Reisemuster der modernen Menschen möglich. Zwar reisen die meisten von uns nur kurze Strecken, doch die wenigen, die weit reisen, können Krankheitserreger in kürzester Zeit weltweit verteilen.

Nicht erst mit Entstehen der Mexikanischen Grippe (oder Schweinegrippe) im April 2009 in Mexiko begannen Physiker mit der Untersuchung von Ausbreitungsmustern von Viren. Die Wege, die Menschen in der heutigen Zeit zurücklegen, folgen nämlich spannenden Mustern, deren Kenntnis für viele Bereiche der Physik und anderer Fachgebiete nützlich ist. So ist die Verbreitung von ansteckenden Krankheiten aus Sicht eines Physikers ein sogenannter Diffusionsprozess, der etwa mit der Vermischung von Schadstoffen in Wasser oder Ausbreitung von Informationen in Datennetzen verwandt ist.

Die Wege, die Viren zurücklegen und zur Ausbreitung von Seuchen oder „Pandemien“ (gemeint sind damit weltweite Epidemien) führen, sind an die Wege der Wirtstiere gekoppelt. Im Fall der Mexikanischen Grippe des Jahres 2009 sind die Wirtstiere Menschen, sodass die Virenwege mit den Reisemustern von Menschen zusammen hängen. Da es unmöglich ist, die Wege von sechs Milliarden Menschen zu verfolgen, bedient man sich eines sogenannten Proxys, also eines Stellvertreters. Was kann im Falle der Viren ein solcher Stellvertreter sein?

Geldscheine als Stellvertreter

Random Walk und Lévy-Flug

Geht man davon aus, dass Viren sowohl mit ihrem Wirt reisen können, als auch von einem Wirt zu einem anderen überspringen, dann ist dies ein Verhalten, das dem von Bargeld entspricht: Auch hier reist ein Geldschein im Portemonnaie, bis er den Besitzer wechselt. Praktischerweise gibt es in den USA ein privat organisiertes Geldscheinverfolgungssystem: Unter http://www.wheresgeorge.com wurden bisher mehr als 150 Millionen Geldscheine eingegeben. Anhand der Seriennummer lassen sich die Reisemuster erkennen. Dabei wird klar: Die Scheine wandern zwar meist mit einer Durchschnittsgeschwindigkeit von knapp unter 4 Meilen pro Tag, aber zuweilen machen sie in kurzer Zeit große Sprünge. Ganz klar: Einer der Besitzer des Scheines unternahm eine längere Reise. Übrigens, auch für die Eurozone gibt es eine solche Geldscheinverfolgung: Unter http://de.eurobilltracker.com wurde allerdings erst 60 Millionen Geldscheine erfasst, mehr als fünf Mal wurde dabei bislang kein Schein wiedergefunden.

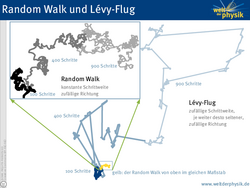
Bei allen Unzulänglichkeiten, die die Geldscheinverfolgung hat, so kann man doch eine Statistik sehr zuverlässig erfassen: Ausgehend von einem Startort von vielen Geldscheinen – wie weit kommen die Scheine in einem bestimmten Zeitraum? Dabei stellt sich heraus: Die meisten Scheine reisen nicht weit, nur eine kleine, aber bedeutende Menge ist auch schon nach einer Woche weit über tausend Kilometer gekommen. Genau diese Statistik lässt sich mit einer bestimmten Sorte zufälliger Wege erreichen: Den sogenannten Lévy-Flügen. Im Gegensatz zu den einfachen Zufallswegen (Random Walk), bei denen jeder Schritt immer gleich lang ist, nur die Richtung komplett zufällig, sind bei Lévy-Flügen auch sehr lange Schritte möglich. Die Wahrscheinlichkeit nimmt dabei mit der Schrittlänge ab, sehr große Schritte sind also sehr unwahrscheinlich – aber eben doch möglich.

Schnelle Ausbreitung durch lange Reisen

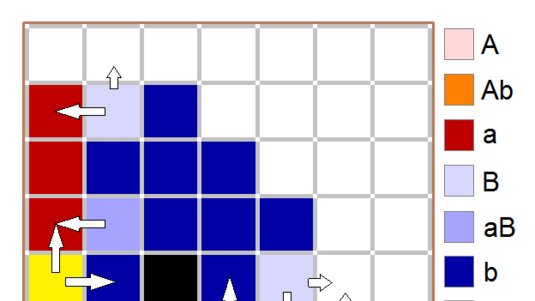
Die genauere Analyse der Lévy-Flüge zeigt, dass die Ausbreitung von Geldscheinen (oder eben Viren mit dem „Wirtstier“ Mensch) ausgehend von einem Ort sehr schnell und nicht geographisch beschränkt geschieht. Man kann für Epidemien mit Hilfe der Randow-Walk-Modelle oder der Lévy-Fluge nun zweidimensionalle Modelle der Ansteckungsrate bzw. der Anzahl der erkrankten Personen simulieren. Eine Krankheit in einer Gesellschaft, die keine weiten Reisen unternimmt, bei denen also Zufallswege der Virenwanderung wie beim Random Walk entscheidend sind, breitet sich in Wellen um den Entstehungsort aus. Eine solche Epidemie war zum Beispiel der „schwarze Tod“, die erste Pandemie im 14. Jahrhundert.

Doch die heutige Situation ist die der Lévy-Flüge. Alle Berechnungen ergeben bei von Mensch zu Mensch übertragenen Krankheiten mit passender Ansteckungsrate eine sehr schnelle globale Verbreitung. Da der globale Reiseverkehr so immens schnell ist und die Menschen dabei in sehr engen Räumen zusammenkommen, sind besonders die Langstreckenreisen nicht nur Transport- sondern auch Ansteckungspunkte.

Mit anderen Methoden als den Diffusionsgleichungen aus den Lévy-Flügen lassen sich auch sehr detaillierte Simulationen von Gegenmaßnahmen gegen Epidemien erstellen. So konnten Wissenschaftler mit Agent-basierten Simulationen im Zusammenhang mit SARS die einzelnen Phasen des Auftretens sehr exakt simulieren. Bei solchen Simulationen werden große Mengen von Personen simuliert und Faktoren wie die Ansteckungsrate, der Gesundheitszustand des Nachbarn, die Tödlichkeit der Krankheit sowie Inkubationszeit und Dauer der Ansteckungsgefahr durch einen infizierten Menschen angepasst. So können die Einflüsse von Quarantäne, Fiebermessung oder das Tragen von Atemschutzmasken auf ihre Wirksamkeit überprüft werden.

Der folgende Film den Dirk Brockmann (Northwestern University, zuvor Max-Planck-Institut für Dynamik und Selbstorganisation, Göttingen) zeigt zwei Simulationen von Epidemien, die in München ausbrechen. Im ersten Fall gibt es nur kurze Reisewege – wie beim schwarzen Tod im Mittelalter. Der zweite Fall zeigt die viel schneller verlaufende moderne Ausbreitung.