Einfluss des Zufalls auf Evolution berechenbar
Bevölkerungsdichte bestimmt die Geschwindigkeit der biologischen Entwicklung
Göttingen - Wissenschaftler vom Max-Planck-Institut für Dynamik und Selbstorganisation in Göttingen berichten von einem mathematischen Verfahren, das es zum ersten Mal ermöglicht den Zufallseinfluss auf die Evolution quantitativ zu erfassen. Mit dem neuen Modell lässt sich nicht nur die Geschwindigkeit der Evolution vorhersagen, sondern auch der Ablauf chemischer Reaktionen oder die Ausbreitung von Seuchen, so der Physiker Oskar Hallatschek.
Mutationen, also Veränderungen des Erbgutes, gehen auf zufällige Prozesse zurück. Eine Mutation kann für den Träger positive, negative oder aber keinerlei Folgen haben. Durch Vererbung kann eine Mutation dann innerhalb einer Population weitergegeben werden. Der Vorteil, den die Mutation seinem Träger bietet beeinflusst schließlich die Selektion. Allerdings können auch gute Gene dem Genpool durch Zufallseinflüsse entzogen werden, etwa wenn der Träger durch einen tödlichen Unfall nicht zur Fortpflanzung kommt.
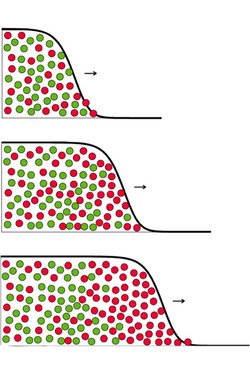
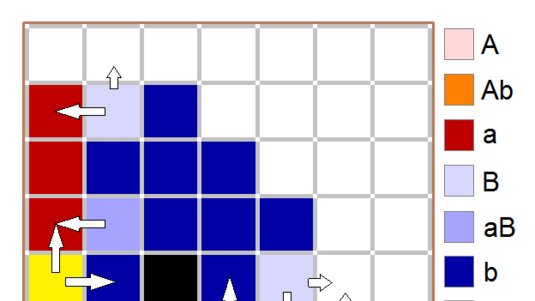
Die Ausbreitung der Mutation hängt davon ab, wer wann mit wem Nachkommen zeugt. Dabei ist das zufallsbestimmte Kontaktknüpfen umso stärkeren Schwankungen unterworfen, je geringer die Bevölkerungsdichte ist. Computersimulationen zeigen, dass sich Mutationen in Form einer Welle über das besiedelte Gebiet ausbreiten, wobei zufällige Fluktuationen zu einer verlangsamten und unregelmäßigen Ausbreitung führen. Wie schnell die Evolution abläuft hängt letztlich davon ab, wie stark eine Mutation die Überlebenschance seines Trägers gegenüber seinen Artgenossen erhöht sowie von der Besiedlungsdichte und der sich daraus ergebenden Anzahl an Kontakten.
Bislang konnte die wellenförmige Ausbreitung einer Mutation nur für den Fall berechnet werden, dass der Zufall im Vergleich zum Selektionsvorteil der Mutanten eine geringe Rolle spielt und somit vernachlässigbar ist. Das Standardmodel für solche wellenartigen Phänomene ist die stochastische Fisher-Kolmogorov-Petrovsky-Piscounov-Gleichung (SFKPP-Gleichung), die das Wachstum, die Ausbreitung und die Zufallsfluktuationen von Lebewesen, aber auch von chemischen Stoffen beschreibt. Da die meisten in der Natur vorkommenden Mutationen aber nur einen geringen Selektionsvorteil bieten, spielt der Zufall in der Realität eine vergleichsweise große Rolle. In diesen Fällen sei es daher wichtig auch den Zufallsterm zu berücksichtigen, betont Hallatschek.
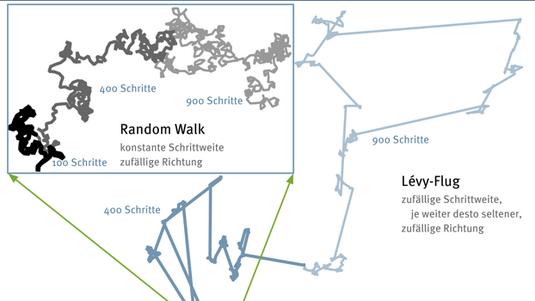
Mit Hilfe eines mathematischen Verfahrens namens Störungsrechnung hat Hallatschek die SFKPP-Gleichung für solche Fälle gelöst. Dabei fand er heraus, dass die Geschwindigkeit der Mutanten-Welle proportional zur Wurzel aus der Bevölkerungsdichte ansteigt. Vervierfacht sich also die Bevölkerung in einer geographischen Region, so breitet sich die Mutation doppelt so schnell aus. Darüber hinaus zeigte er, dass die Längen der Wellenfronten einer Häufigkeitsverteilung folgen, die sich mit einem Potenzgesetz beschreiben lässt. Das Aufspalten der Wellenfront hingegen folgt einem zufallsabhängigen Prozess namens random walk.
Von Populationsgenetik bis Teilchenphysik - in der Natur gibt es viele Prozesse, die sich mit Hilfe der SFKPP-Gleichung beschreiben lassen, so dass das neue Verfahren in Zukunft in ganz unterschiedlichen Bereichen von Nutzen sein wird.
Ziel der Forscher in Göttingen ist es nun die Evolution des Menschen in den letzten 200.000 Jahren anhand von genetischen Daten zu rekonstruieren.
Welt der Physik
Quelle: https://www.weltderphysik.de/gebiet/leben/nachrichten/2009/einfluss-des-zufalls-auf-evolution-berechenbar/