MICROSCOPE: Äquivalenzprinzip im Weltraumtest
Daniel Hagedorn, Hanns Selig

Seit Jahrhunderten bildet das physikalische Gesetz der Gleichheit von schwerer und träger Masse das Fundament der Physik. Nahezu alle Theorien der Physik fußen direkt oder indirekt auf diesem sogenannten Äquivalenzprinzip. Sollte es sich als falsch erweisen, würde unter anderem Einsteins Allgemeine Relativitätstheorie nicht mehr funktionieren. Das Äquivalenzprinzip soll nun im Rahmen der europäischen Weltraummission MICROSCOPE überprüft werden.
Die ursprüngliche Formulierung des Äquivalenzprinzips geht auf eine Annahme von Galileo Galilei im 17. Jahrhundert zurück. Er postulierte die Gleichheit von schwerer und träger Masse. Die schwere Masse unterliegt der Gewichtskraft – sie sorgt also dafür, dass Gegenstände auf der Erde nach unten fallen, eben „schwer“ sind. Der Widerstand eines Körpers gegen eine Kraft, die versucht, seinen Bewegungszustand zu ändern, stellt dagegen die träge Masse dar. Oder alltagsnäher formuliert: Fällt man auf den Boden, verursacht die schwere Masse den Schmerz, rennt man gegen eine Wand, löst die träge Masse das Ungemach aus.
Aus dem Äquivalenzprinzip folgt außerdem, dass alle Objekte, die einem bestimmten Schwerefeld ausgesetzt sind, derselben Beschleunigung unterliegen. Das heißt, das Verhältnis zwischen Gravitationskraft und Masse des Körpers ist konstant. Dieses Prinzip, welches von Galilei formuliert und von Newton übernommen wurde, ist heute mit einer Genauigkeit von bis zu 10-13 überprüft und stellt eine der Grundannahmen von Einsteins Relativitätstheorie dar: Alle Testteilchen werden an einem identischen Ort in der Raumzeit in einem vorgegebenen Gravitationsfeld identisch beschleunigt. Die Beschleunigung ist unabhängig von den Eigenschaften des Teilchens, wie etwa der chemischen Zusammensetzung, der Größe, der Form oder der Masse. Dies gilt auch für die Ruhemasse.
Das Äquivalenzprinzip auf dem Prüfstand
Neuere Theorien, und hier sind vor allem die String-Theorie und die Supergravitationstheorie zu nennen, könnten darauf hinweisen, dass das Äquivalenzprinzip unterhalb einer Messungenauigkeit von 10-13 verletzt sein kann. Die derzeit genaueste Messung mit Daten des Hubble-Weltraumteleskops liegt genau bei dieser Grenze. Um die Verletzung des Äquivalenzprinzips nachzuweisen, sind also noch exaktere Messungen notwendig, die die Genauigkeit von bis zu 10-13 unterschreiten. Hier setzt die Weltraummission MICROSCOPE an: Bei diesem Experiment kann eine Verletzung des Äquivalenzprinzips mit einer Genauigkeit von 10-15 erkannt werden.
Im Rahmen dieses Projekts werden erste Vortests im Fallturm des Zentrums für angewandte Raumfahrttechnologie und Mikrogravitation (ZARM) in Bremen durchgeführt. Nach erfolgreichem Abschluss ist für 2016 der Start der Mission an Bord eines französischen Forschungssatelliten geplant. MICROSCOPE steht für „MICROsatellite à Traînée Compensée pour l'Observation du Principe d'Equivalence“, auf Deutsch etwa: „Kleinstsatellit zur Erkundung von Beobachtungsmöglichkeiten des Äquivalenzprinzips“. Die Mission ist ein Gemeinschaftsprojekt der französischen Weltraumagentur CNES, des französisch-öffentlichen Forschungsunternehmens ONERA, des Deutschen Zentrums für Luft- und Raumfahrt (DLR), der Physikalisch-Technischen-Bundesanstalt (PTB) in Braunschweig, des ZARM der Universität Bremen und der europäischen Weltraumorganisation ESA.
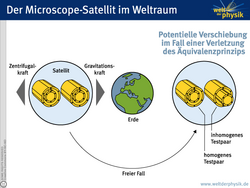
Mithilfe dieses Weltraumexperiments soll nun noch genauer überprüft werden, ob das Äquivalenzprinzip zutrifft und ob es universelle Gültigkeit besitzt. Dies ist durch Messung der Beschleunigungen von zwei Testmassen möglich, die gleichermaßen sowohl der Gravitationskraft – die auf die schwere Masse wirkt – als auch der Zentrifugalkraft – die auf die träge Masse wirkt – ausgesetzt werden. Wenn nun die Beschleunigungen dieser Testmassen voneinander abweichen würden, wäre das Äquivalenzprinzip widerlegt und die schwere Masse wäre nicht mehr mit der trägen gleichzusetzen. Für ein erfolgreiches Experiment müssen die beiden Testmassen zur gleichen Zeit am gleichen Ort die gleiche Kraft sowohl durch Gravitation als auch durch Zentrifugalkraft erfahren. Dazu geht man in den Erdorbit, denn für den Satellitenflug gilt genau dies: Der Betrag der Zentrifugalkraft ist gleich dem der Gravitationskraft.
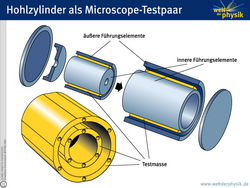
Außerdem braucht man noch einen weiteren Trick, um zwei Massen an den gleichen Ort zu bringen: Man baut eine kleine Testmasse in eine große ein. Damit sind die Massen zwar nicht am gleichen Ort, wohl aber ihr geometrisches Zentrum sowie das Zentrum des sogenannten Trägheitstensors, der etwa die Mitte der Trägheitswirkung beschreibt. Als Testmassen bieten sich somit Hohlzylinder an. Um die Zentren der Körper so präzise wie möglich überdecken zu können, muss die Dichte der Testmassen homogen und ihre Form sehr genau gefertigt und bekannt sein.
Bei MICROSCOPE wird es zwei Paare von Testmassen geben: Eines wird homogen bestückt sein, mit zwei Testmassen, die aus demselben Material bestehen. Dieser homogen aufgebaute Beschleunigungsaufnehmer dient als Referenz, um den Einfluss des Messinstruments auszuschließen. Ein zweites Paar wird mit Testmassen bestückt werden, die aus verschiedenen Materialien mit sehr unterschiedlichen Dichten bestehen. Mit diesem Aufbau soll nun überprüft werden, ob eine Abweichung vom Äquivalenzprinzip existiert, also unterschiedliche Materialien unterschiedlich auf Trägheitskraft und Gravitation reagieren.
Schwere Masse gleich träge Masse?
Die Testmassen werden innerhalb eines Satelliten installiert, der sich auf einer Kreisbahn um die Erde bewegt. Auf den Satelliten und seinen Inhalt wirken gleichermaßen die Zentrifugalkraft, welche die Objekte nach außen von der Erde weg, und die Erdanziehung, die in die Gegenrichtung „zieht“. Durch das Kräftegleichgewicht befinden sich die Objekte innerhalb des Satelliten im Schwebezustand – sie befinden sich also im freien Fall als permanentem Zustand. Oder anders formuliert: Die Testmassen fallen quasi „um die Erde herum“.
Im MICROSCOPE-Experiment soll nun überprüft werden, ob sich die Zylinder des heterogenen Paars nach einer langen „Fallzeit“ gegeneinander zu verschieben „versuchen“, die Hohlkörper des homogenen Paars aber einfach exakt ineinander liegen bleiben. Sollte nämlich die Gravitationskraft doch unterschiedlich auf verschiedene Materialien wirken, so würde dies nach einer gewissen Zeitspanne dadurch zutage treten, dass die Testmassen des heterogenen Zylinderpaars auseinander streben würden (siehe Abbildung) und nur durch die Aufwendung elektrostatischer Kräfte auf ihrer Position gehalten werden könnten. Dies hieße aber, dass die „schwere Masse“ eine Eigenschaft ist, die auch von der Zusammensetzung des Materials abhängt und somit nicht mehr mit der „trägen Masse“ gleichzusetzen ist. Wenn das Äquivalenzprinzip stimmt, sollte hingegen jedes Paar der Testmassen perfekt zum anderen ausgerichtet bleiben, während sie die Erde umkreisen – ohne dass dafür zusätzliche Kräfte aufgewendet werden müssten.
Dieser komplizierte Aufbau ist ein spezielles Charakteristikum des MICROSCOPE-Expertiments: Bei anderen geplanten Weltraummissionen zur Überprüfung des Äquivalenzprinzips wie beispielsweise STEP tritt die Verletzung des Prinzips durch eine reale Verschiebung der inhomogenen Testmassen zueinander zutage. Bei MICROSCOPE hingegen werden die beiden Testmassen des inhomogenen Paares von elektrostatischen Kräften auf ihrer Position gehalten, bevor sie sich gegeneinander verschieben können. Das heißt, die Verschiebung findet real gar nicht statt. Man misst nur die Kräfte, die aufgewendet werden müssen, um die Testmassen an einer möglichen Verschiebung zu hindern. Indikator für eine Verletzung des Äquivalenzprinzips ist also keine real stattfindende Verschiebung, sondern nur der „Versuch“ einer Verschiebung. Dennoch ist in der nebenstehenden Abbildung die potenzielle Verschiebung zum besseren Verständnis abgebildet.
Sollten die Messergebnisse im Widerspruch zum Äquivalenzprinzip stehen, könnte dies auf das Wirken einer neuen, noch unbekannten Naturkraft oder Erscheinung hindeuten und damit unser Wissen über das Wesen der Gravitation und der Naturgesetze erheblich erweitern. Wenn das Äquivalenzprinzip also unterhalb einer messbaren Grenze verletzt ist, hat dies für die Physik kaum abzuschätzende Folgen. Sämtliche Theorien, die auf diesem Prinzip aufbauen, müssten verworfen oder neu geschrieben werden – vielleicht wären die Ergebnisse erste experimentelle Indizien für die Gültigkeit von Stringtheorien.
Über die Jahrhunderte wurde die Gültigkeit des Äquivalenzprinzips von zahlreichen namhaften Physikern überprüft. Die Überprüfung erfolgt, indem die Beschleunigungen zweier unterschiedlicher Körper experimentell bestimmt werden. Hieraus lässt sich eine Größe bestimmen, die in der Physik als das Eötvös-Verhältnis \(\eta\) bekannt ist. \(\eta\) stellt ein Maß für die Genauigkeit dar, mit welcher das Äquivalenzprinzip überprüft wurde.
Loránd Eötvös (1848-1919) war ein ungarischer Physiker, der eine Drehwaage entwickelte, welche die Richtigkeit des Äquivalenzprinzips mit bis dato unerreichter Genauigkeit bestätigen konnte. Er definierte die Größe \(\eta\) („Eta“) zu:
$$\eta=\frac{2|a_1-a_2|}{|a_1+a_2|}$$
also dem Verhältnis der Differenzen der gemessenen Beschleunigungen zweier homogener Testkörper zu der Summe der Beschleunigungen. Dieses Verhältnis gibt die Genauigkeit der Messmethode an, mit der eine Abweichung der Beschleunigung von einer Testmasse relativ zur Beschleunigung der anderen Testmasse überhaupt festgestellt werden kann. Falls nun die Differenz zwischen den beiden Beschleunigungen geringer ist als die Genauigkeit der Messung, ist das Experiment ohne Aussagekraft. Da die Stringtheorie eine Abweichung voraussagt, die unter 10-13 liegt, kann diese Aussage nur durch eine Messung, die eine noch geringere Ungenauigkeit aufweist, widerlegt oder verifiziert werden. Wenn das MICROSCOPE-Experiment hält, was angestrebt wird, und eine Messung mit einer Genauigkeit von 10-15 ermöglicht, wäre das Ergebnis zukunftsweisend. Sollte keine Abweichung der Beschleunigungen gemessen werden, bliebe alles wie gehabt – zumindest bis noch genauere Messungen zu einem anderen Ergebnis kämen. Falls aber doch eine Differenz der Beschleunigungen gemessen wird, würde dies nicht nur das Äquivalenzprinzip widerlegen, sondern auch den Stringtheoretikern experimentellen Rückhalt verschaffen.
Das Äquivalenzprinzip wurde unter anderem überprüft von:
Galileo (1638), Newton (1689), Bessel (1832): | \(\eta<10^{-3}\) |
Eötvös – Drehwaage (1909): | \(\eta<10^{-9}\) |
Dave Scott – Show-Experiment, Apollo 15 (1970) | |
Shapiro – Lunar Laser Ranging (1976): | \(\eta<10^{-12}\) |
Adelsberger – Hubble-Weltraumteleskop (1999): | \(\eta<10^{-13}\) |
Die vier Erstgenannten nutzten Fallexperimente oder mechanische Aufbauten (schiefe Ebenen, Drehwaage), um \(\eta\) zu bestimmen. Dave Scott ist ein US-Astronaut, der während der Apollo-15-Mission auf dem Mond TV-gerecht einen Hammer und eine Feder fallen ließ. (Dieses Experiment ist der vielleicht beste Beweis, dass die Amerikaner wirklich auf dem Mond waren.) Irwin Shapiro nutzte eine optische Methode zur Bestimmung von \(\eta\): Neben Fußabdrücken ließen die Apollo-Astronauten nämlich auch Laser-Reflektoren auf dem Mond zurück, mit deren Hilfe interferometrisch der Abstand zwischen Erde und Mond gemessen wird. Aus diesen Daten konnte Shapiro \(\eta\) mit einer Unsicherheit von 10-12 bestimmen. 10-12 ist auch die beste, messtechnisch erreichbare Unsicherheit für erdgestützte Experimente. Der Grund hierfür sind Störungen wie Erdbeben, Gezeitenkräfte, Luftbewegungen, Temperaturschwankungen und vieles mehr. Um genauer zu werden, müssen die Experimente im Weltraum durchgeführt werden. Hier berechnete Adelsberger im Jahre 1999 aus Daten, die mit dem Hubble-Weltraumteleskop gewonnen wurden, den bislang genauesten Wert von \(\eta\): 10-13. Allerdings ist die verwendete Methode unter Wissenschaftlern umstritten.
Im Rahmen des Microscope-Experiments soll nun \(\eta\) mit einer Genauigkeit von 10-15 bestimmt werden. Auch andere Weltraummissionen sind geplant: Zu nennen ist hier noch die STEP-Mission (Satellite Test of the Equivalence Principle), welche durch Beschleunigungsexperimente von vier Testmassen eine \(\eta\)-Genauigkeit von 10-18 liefern soll. Allerdings stellt deren Durchführung für die NASA wegen der anstehenden Mond- und Marsflüge keine Priorität dar.
An den Missionen MICROSCOPE und STEP ist die Physikalisch-Technische Bundesanstalt (PTB) im Rahmen der Entwicklung einer Herstellungstechnologie für die in den Experimenten verwendeten Testmassen sowie deren Fertigung als Projektpartner beteiligt. Um \(\eta\) zu bestimmen, müssen die Beschleunigungen von zwei Testmassen gemessen werden. Für ein erfolgreiches Experiment müssen die zwei Testmassen zur gleichen Zeit am gleichen Ort die gleiche Kraft erfahren. Um die Zentren der Körper so präzise wie möglich überdecken zu können, muss die Dichte der Testmassen homogen und ihre Form sehr genau gefertigt und bekannt sein. In beiden Bereichen hat die PTB über hundert Jahre Erfahrung und diese ist auch notwendig, denn die Anforderungen sind extrem hoch. Die hauptsächliche Schwierigkeit bei der präzisen Fertigung der Testmassen besteht in deren Dreidimensionalität. Solch eine Fertigung ist Neuland.
Eine der größten Herausforderungen war laut Daniel Hagedorn, Ansprechpartner der PTB für die MICROSCOPE-Mission, die Vermessung der Testmassen in der Werkzeugmaschine. Gerade während der kritischen Endfertigung kann die Testmasse nicht aus der Maschine genommen werden. Also ist es nicht möglich, sie außerhalb zu vermessen. Die PTB entwickelte nun ein Verfahren, welches eine Messung innerhalb der Werkzeugmaschine ermöglicht, die den Anforderungen im Mikrometerbereich gerecht wird.
Die Beschleunigungsmesser des MICROSCOPE-Satelliten werden am Fallturm des ZARM im freien Fall getestet. Dies ist die einzige Möglichkeit, die Funktionsweise der komplexen Instrumente auf der Erde zu überprüfen, so Hanns Selig, Projektleiter am ZARM.
Während des knapp fünf Sekunden dauernden freien Falls können die Sensoreigenschaften und die Performance sehr genau getestet werden. Hierfür finden insgesamt etwa einhundert Freifallversuche statt, bevor baugleiche Instrumente dann in den Satelliten installiert werden. Darüber hinaus wird am ZARM in einem Team von Physikern und Ingenieuren eine komplette Missionssimulation am Computer durchgeführt. So können bereits vor dem Start der Mission verschiedene Szenarien durchgespielt werden. Das hilft, die Prozeduren für die Analyse der wissenschaftlichen Daten zu optimieren.
Welt der Physik CC by-nc-nd
Quelle: https://www.weltderphysik.de/gebiet/universum/teleskope-und-satelliten/microscope/