Warum Neutronen schwerer sind als Protonen
Jan Oliver Löfken
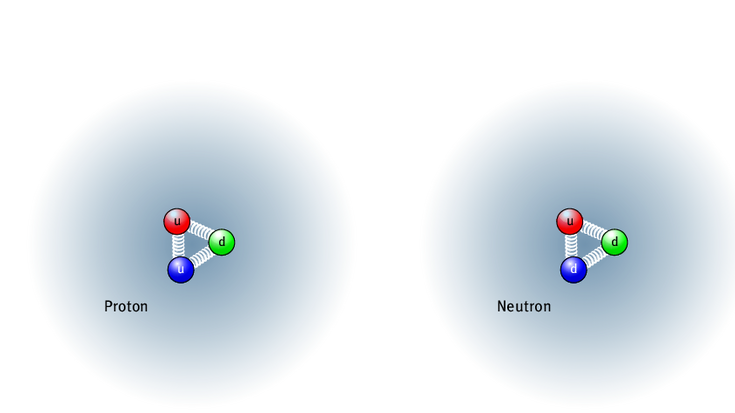
Alle Atomkerne bestehen aus Neutronen und Protonen. Ein Neutron ist dabei ein wenig schwerer als ein Proton. Mit neuen Berechnungen auf der Basis der gültigen Modelle konnte ein Team um Szabolcs Borsányi von der Universität Wuppertal diesen Unterschied mit der bisher höchsten Genauigkeit bestimmen. Wie die Physiker in der Fachzeitschrift „Science“ berichten, ließen sich damit auch die Ursachen für die unterschiedliche Masse von Proton und Neutron näher erklären.
„Unsere Existenz hängt von dieser winzigen Massendifferenz ab“, sagt Koautor Zoltán Fodor von der Eötvös Universität in Budapest, der derzeit an der Universität Wuppertal arbeitet. Wäre das Neutron um mehr als 1,3 Megaelektronenvolt/c2, der gängigen Einheit für die Teilchenmasse, schwerer als das Proton, wären die Fusionsprozesse in den Sternen und die Bildung von schweren Elementen deutlich unwahrscheinlicher. Wäre das Neutron hingegen leichter als beobachtet, wären Wasserstoffatome instabil. Um die Massendifferenz genauer zu ermitteln, führten Borsányi und seine Kollegen umfangreiche Berechnungen durch.
Diese Computersimulationen basierten auf den zwei grundlegenden Theorien der Teilchenphysik: der Quantenchromodynamik und der Quantenelektrodynamik. Dabei beachteten die Forscher nicht nur den Aufbau von Neutron und Proton aus zwei Down-Quarks und einem Up-Quark respektive einem Down-Quark und zwei Up-Quarks. Auch die in den Teilchen wirkenden Kräfte gingen mit hoher Präzision in die Rechnungen ein. Das Ergebnis: Die Ungenauigkeit für den Massenunterschied beträgt nur noch 0,3 Megaelektronenvolt/c2.
Verantwortlich für den Massenunterschied machen die Forscher die Wechselwirkung von mehr oder weniger starken Kräften im jeweiligen Quarktriplett. In ihren Simulationen berücksichtigten sie die relativ weitreichenden elektromagnetischen Kräfte und die Auswirkungen des sogenannten Isospins der beteiligten Quarks. Der Isospin ist eine Quantenzahl, um die Symmetrie von Teilchen unter der nicht weitreichenden, starken Wechselwirkung zu beschreiben. Beide Komponenten führten schließlich zu dem genauen Ergebnis, das sehr gut mit experimentellen Massenbestimmungen von Neutron und Proton übereinstimmt.
Wissenschaft aktuell gemäß den Bedingungen der Quelle
Quelle: https://www.weltderphysik.de/gebiet/teilchen/nachrichten/2015/warum-neutronen-schwerer-sind-als-protonen/