Die Suche nach dem Higgs-Boson und dem Ursprung der Masse

1964 postulierten der britische Physiker Peter Higgs und Kollegen das Higgs-Boson. Seitdem befinden sich weltweit Teilchenphysiker auf einer fieberhaften Suche nach einem Teilchen, das die Existenz von Masse in unserem Universum erklären soll.

Spätestens seitdem Experimente an Teilchenbeschleunigern in Europa und den USA (LEP und Tevatron) indirekt Indizien für die Existenz des Higgs-Teilchens gefunden haben, bildet die Higgs-Suche eine zentrale Aufgabe der modernen Teilchenphysik. Doch warum ersehnen viele Teilchenphysiker dieses neue Teilchen? Was lässt sich mit dem Higgs-Mechanismus erklären? Und wie kann man am Large Hadron Collider LHC nach langen Jahren der vergeblichen Suche endlich fündig werden?

Was ist eigentlich „Masse“?

In der Physik unterscheiden wir zwei Arten von Masse: schwere und träge Masse. Schwere Massen erkennen wir daran, dass sie sich anziehen. Körper mit schwerer Masse fallen daher beispielsweise auf den Boden, da sie von der schweren Masse der Erde angezogen werden. Träge Masse hingegen äußert sich darin, dass man Kraft aufwenden muss, um sie in Bewegung zu versetzen oder abzubremsen. Nach dem Einstein'schen Äquivalenzprinzip sind allerdings die schwere Masse und die träge Masse eines Körpers identisch.

Die Teilchen im Standard-Modell

Die Beobachtung zeigt, dass fast alle bekannten Elementarteilchen eine träge Masse besitzen. Für die Beschreibung der Elementarteilchen und der zwischen ihnen wirkenden Kräfte stellt sich jedoch heraus, dass die Berücksichtigung ihrer Masse in den Bewegungsgleichungen ein massives Problem mit sich bringt: Die Eigenschaft Masse stört das Symmetrieprinzip (das sogenannte Eichprinzip) aus dem sich eben diese Bewegungsgleichungen herleiten lassen. Dieses Symmetrieprinzip funktioniert so wunderbar, dass sämtliche Messungen der Kräfte zwischen Elementarteilchen mit ihm erklärbar sind – es fällt also schwer, dieses so gut funktionierende Konzept völlig aufzugeben. Und selbst wenn man hierzu bereit wäre, führt die Berücksichtigung der Masse in den Bewegungsgleichungen der Teilchen bei hohen Energien zu sinnlosen Ergebnissen: Die Wahrscheinlichkeit, dass zwei massive Teilchen miteinander wechselwirken, steigt dann über alle Grenzen, wird also irgendwann größer als eins – ein unmögliches Resultat.

Ausweg Higgs-Mechanismus

Auf den ersten Blick erscheint der Rettungsplan für das Eichprinzip bizarr: Es wird die Hypothese aufgestellt, dass die Elementarteilchen die Eigenschaft „Masse“ gar nicht besitzen. Das Eichprinzip ist dann gerettet und alle Kräfte zwischen den Teilchen werden korrekt und widerspruchsfrei beschrieben – auch bei hohen Energien. Nun müssen wir „nur noch“ erklären, warum unsere Messungen ergeben, dass sich die meisten Teilchen so verhalten, als hätten sie Masse, obwohl wir sie doch als masselos angenommen haben.

An dieser Stelle lohnt es sich, eine alternative Definition der Eigenschaft „Masse“ anzuschauen: Da sich nur masselose Teilchen im Vakuum mit Lichtgeschwindigkeit bewegen, könnte man ein Teilchen mit Masse als ein Teilchen definieren, das sich im Vakuum langsamer als mit Lichtgeschwindigkeit bewegt.

Der Trick liegt an der Einschränkung „im Vakuum“: Die zentrale Hypothese des Higgs-Mechanismus ist die, dass das, was wir als „leeren Raum“, also als Vakuum erfahren, gar nicht leer ist. Der gesamte „leere Raum“, so wird postuliert, ist angefüllt mit einem Feld, dem Higgs-Feld. Alle Teilchen, die dieses Feld spüren, verändern ihre freie Bewegung, so dass sich die Teilchen eben nicht mehr mit Lichtgeschwindigkeit, sondern langsamer bewegen. Teilchen, die das Higgs-Feld spüren, verhalten sich also so, als hätten sie die Eigenschaft „Masse“ obwohl sie eigentlich (das heißt in einem wirklich leeren Raum) masselos sind.

Gewicht und Auftrieb als Analogon

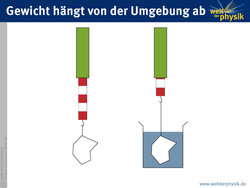
„Masse“ ist in diesem Modell also nicht mehr eine Eigenschaft eines Teilchens, sondern das Resultat seiner Wechselwirkung mit dem Higgs-Feld. Je stärker die Wechselwirkung eines Teilchens mit dem Higgs-Feld ist, desto größer ist seine scheinbare Masse. Das lässt sich vergleichen mit einem Stein, der aufgrund des Auftriebs unter Wasser leichter erscheint als in Luft. Das Higgs-Feld sorgt jedoch nicht für eine scheinbare Abnahme der Gewichtskraft, sondern für eine scheinbare Zunahme der trägen Masse. Postuliert man nun, dass die verschiedenen Teilchen unterschiedliche Wechselwirkungsstärken mit dem Higgs-Feld haben, so lassen sich die verschiedenen (scheinbaren) Massen der Teilchen „erklären“.

Der Preis: das Higgs-Teilchen

Es ist nicht schwer, im theoretischen Modell ein Feld einzuführen, das den leeren Raum so verändert, dass die Teilchen eine scheinbare Masse erhalten. Allerdings ergeben sich aus den naivsten Ansätzen schnell neue Widersprüche. Die Kunst bestand darin, das Higgs-Feld so in die Theorie einzufügen, dass es selbst dem grundlegenden Eichprinzip genügt. Denn dieses Prinzip will man ja gerade retten.

Die Eigenschaften eines solchen Feldes zu konstruieren, war die Leistung von Peter Higgs (und anderen): Das Higgs-Feld hat einen sogenannten Vakuumerwartungswert. Es wechselwirkt im leeren Raum mit den Teilchen, aber gehorcht dabei dennoch dem Eichprinzip. Der Preis für dieses Higgs-Feld: Es ist zwingend verbunden mit der Existenz eines neuen Elementarteilchens, des Higgs-Bosons.

Die Entdeckung des Higgs-Bosons würde das Phänomen „Masse“ erklären und als Wechselwirkung mit dem (gefüllten) Vakuum enttarnen. Bislang hat niemand ein solches Higgs-Boson beobachtet – das widerlegt jedoch die Hypothese des Higgs-Mechanismus noch nicht. Denn auch das Higgs-Boson hat eine Masse, die es aus der Wechselwirkung mit seinem eigenen Vakuumfeld erhält. Daher könnte das Higgs-Boson einfach zu massiv sein, um in bisherigen Teilchenphysikexperimenten nachgewiesen werden zu können.

Erste Anzeichen?

Leider kann die Masse des Higgs-Bosons nicht genau vorhergesagt werden. Aus den Experimenten am Beschleuniger LEP – einem der Vorgänger des LHC – wissen wir jedoch, dass seine Masse größer als 114 GeV/c² sein muss (etwa die Masse eines Silberatoms). Ansonsten hätte es sich dort zeigen müssen.

Doch möglicherweise hat das Higgs-Boson schon bei LEP seine ersten Spuren hinterlassen. Denn die Messungen von Teilchenreaktionen, die an den LEP-Experimenten beobachtet wurden, waren so präzise, dass bei ihnen Beiträge eines etwaigen Higgs-Bosons berücksichtigt werden müssen. Die Messungen sind kompatibel mit einem Higgs-Boson, das leichter als etwa 200 GeV/c² ist. Sie stellen einen überzeugenden ersten Hinweis auf das Higgs-Boson dar. Denn Modelle, die ohne den Higgs-Mechanismus auszukommen versuchen, haben größte Schwierigkeiten, diese Präzisionsmessungen zu erklären, wenngleich die Messungen natürlich noch keinen Beweis für den Higgs-Mechanismus darstellen.

Allerdings wissen wir auch, dass das Higgs-Boson nicht schwerer als etwa 700 bis 1000 GeV/c² sein kann, da es sonst die schon angesprochenen Probleme mit der Wahrscheinlichkeitserhaltung nicht lösen und somit seinen Sinn verlieren würde. Am Large Hadron Collider LHC haben wir damit die Möglichkeit, das Higgs-Boson zu entdecken. Im Gegensatz zu allen anderen vorherigen Beschleunigern kann der LHC den gesamten theoretisch möglichen Massenbereich nach dem Higgs-Teilchen durchsuchen. Damit wird der Higgs-Mechanismus zur Erklärung des Phänomens „Masse“ in den nächsten Jahren entweder bestätigt oder ein für alle Mal widerlegt.

Woran erkennt man ein Higgs-Boson?

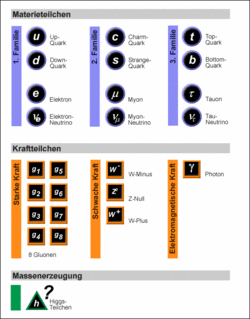
Am LHC werden Protonen bei einer Energie von geweils 7000 GeV (7 TeV) zur Kollision gebracht. Da Protonen jedoch zusammengesetzte Objekte sind, stehen die Protonen nicht als Ganzes für die Erzeugung neuer Teilchen zur Verfügung. Vielmehr sind es die Bestandteile des Protons, die Quarks und Gluonen, die die eigentlichen Stoßpartner darstellen. In der weit überwiegenden Mehrheit aller Fälle werden bei diesen Kollisionen von Quarks und Gluonen bereits bekannte Prozesse stattfinden.

Sollte das Higgs-Boson existieren, so kommt es sehr selten vor, dass zwei Gluonen kurzzeitig zu einem Higgs-Boson verschmelzen. Dieser Prozess passiert in etwa zehn Milliarden Proton-Proton-Kollisionen nur einmal. Dabei ist das Problem nicht, dass zu wenige Higgs-Bosonen produziert würden – die erwartete Erzeugungsrate beträgt immerhin ein bis zehn Higgs-Bosonen pro Sekunde. Vielmehr liegt die Schwierigkeit darin, ein Higgs-Ereignis aus den zehn Milliarden Nicht-Higgs-Ereignissen herauszufischen.

Woran erkennt man also ein Higgs-Boson? Higgs-Bosonen zerfallen praktisch sofort (nach etwa 10^-22 Sekunden) wieder in bekannte Teilchen – im von den LEP-Experimenten bevorzugten Bereich für die Higgs-Masse, zu etwa achtzig Prozent in die schweren b-Quarks. Zwar lassen sich b-Quarks am LHC gut identifizieren, aber sie sind auch in anderen Prozessen so omnipräsent, dass b-Quarks aus Higgs-Zerfällen nicht zu isolieren sind.

Simulation: Higgs-Zerfall

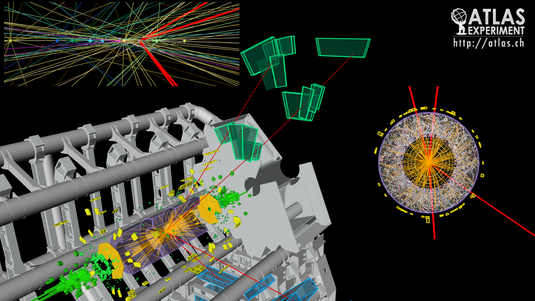
Die Suche konzentriert sich daher auf gut identifizierbare Higgs-Zerfälle, die aber leider wesentlich seltener sind. Für leichte Higgs-Bosonen ist der Zerfall in ein Paar von hochenergetischen Photonen viel versprechend. Photonen lassen sich recht gut identifizieren und vor allem lassen sich sowohl ihre Energie als auch ihre Richtung genau messen. Aus diesen Informationen lässt sich die Masse des hypothetischen Mutterteilchens berechnen. Findet man also einen Überschuss solcher Photonenpaare, die alle auf die gleiche Masse eines Mutterteilchens hinweisen, so ist dies ein guter Hinweis auf die Produktion eines neuen Teilchens. In ähnlicher Weise wurde am CERN-Beschleuniger SppS im Jahr 1984 das Z-Boson im Zerfall in ein Elektron-Positron-Paar entdeckt. Leider passiert einer solcher Zerfall in ein Photonenpaar jedoch nur in etwa einem von tausend Higgs-Zerfällen, so dass man entsprechend lange Daten sammeln muss.

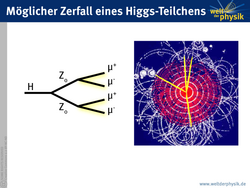
Weitere Suchen nutzen den Zerfall des Higgs-Bosons in ein Paar von Tau-Leptonen aus. Sollte das Higgs-Boson schwerer als etwa 140 GeV/c² sein, so bietet der Zerfall in ein Paar von Z-Bosonen, die wiederum jeweils ein Elektron- oder Myon-Paar zerfallen können, eine sichere Signatur für die Higgs-Entdeckung. Schnell wird es mit der Entdeckung des Higgs-Bosons nicht gehen. Man rechnet mit einer Zeit von mindestens zwei bis drei Jahren der Datennahme, bis die nötige Kalibration der Detektoren abgeschlossen ist und genügend Daten gesammelt sind. Erst dann kann das Higgs-Boson entdeckt oder ausgeschlossen werden.

Alternativen?

Sollte sich das Higgs-Boson, so wie es vom Standardmodell in seiner einfachsten Form vorhergesagt wird, nicht finden, gibt es zunächst die Möglichkeit, dass sich die „massespendende“ Eigenschaft auf mehrere neue Higgs-Bosonen verteilt. Es könnte also gleich eine ganze Familie von Higgs-Bosonen entdeckt werden. Viele solcher Szenarien wurden für den LHC untersucht, mit dem Ergebnis, dass meistens wenigstens eines dieser neuen Teilchen entdeckt werden kann. Eine hundertprozentige Entdeckungsgarantie gibt es in solchen Modellen allerdings nicht. Spekulativ wurde beispielsweise ein ganzes Kontinuum neuer Higgs-artiger Zustände postuliert, ein Szenario, das sich wohl erst an einem neuen Elektron-Positron-Linearcollider ausschließen (oder bestätigen) ließe.

Wenn sich nun überhaupt keine Hinweise auf Higgs-Bosonen am LHC ergeben sollten, bleibt das oben angesprochene Problem mit der Wahrscheinlichkeitserhaltung. Nach mehreren Jahren der Datennahme kann am LHC auch untersucht werden, wie die Natur dieses Problem regelt.

Selbst wenn wir keine sehr überzeugenden Lösungsansätze für eine Higgs-lose (higgsless) Natur haben, eines ist klar: Die Streuung von elementaren Teilchen bei den höchsten am LHC zugänglichen Energien wird uns hierzu wichtige Einblicke geben. In diesem Sinne ist die „Entdeckung“ der Abwesenheit des Higgs-Mechanismus sicher nicht nur eine gewisse Enttäuschung, sondern auch die spannende Möglichkeit, grundlegend Neues über die Mikrophysik zu lernen – auch wenn die Theorie dann sicherlich großen Nachholbedarf hätte.