Die Physik zwischen Fisch und Wasser
Nora Kusche
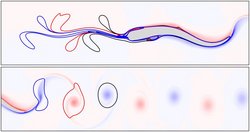
Auch wenn es aussieht, als würden Fische mühelos durch das Wasser gleiten – ihre Fortbewegung gilt physikalisch als Arbeit. Die kleinen Wirbel, die sie auf ihrem Weg durch das Wasser erzeugen, sind Nachweis eines konstanten Impulsaustauschs zwischen Schwimmendem und Umgebung. Wie dieser Fortbewegungsmechanismus funktioniert, ist zumindest im Detail noch nicht verstanden.
Die Kraft, mit der zwei klar abgegrenzte Festkörper aufeinander wirken, lässt sich relativ einfach berechnen. Wichtig ist, an welcher Stelle welcher Impuls übertragen wird. Wenn ein Körper von einer Flüssigkeit wie Wasser oder Luft umgeben ist, ist das nicht immer eindeutig auszumachen. Deshalb hat ein Forscherteam um Florian Huhn von der Eidgenössischen Technischen Hochschule Zürich versucht, die Komplexität von Geschwindigkeitsfeldern in Flüssigkeiten zu reduzieren. In Simulationen betrachten die Forscher die Strömungswirbel um einen Fisch jeweils als eigene in sich abgeschlossene Einheiten – anstatt den Wasserstrom als Ganzes zu untersuchen. Ihre Methode haben die Forscher nun in der Fachzeitschrift „Chaos“ beschrieben.
„Vögel, Fische und Insekten verändern alle das Medium, durch das sie sich bewegen. Mit unserer Methode wollen wir diese Veränderung möglichst einfach erklären und dafür müssen wir einzelne Wirbel in der Strömung ausmachen und extrahieren“, sagt Erstautor Florian Huhn im Gespräch mit Welt der Physik. Die Forscher beschreiben die Impulsübertragung zwischen Wasser und schwimmendem Fisch mithilfe von komplexen, raumzeitlichen Wirbelfeldern, den sogenannten kohärenten Lagrange’schen Strukturen. Das sind Muster langlebiger, zusammenhängender Bewegungen von Flüssigkeiten oder Gasen in turbulenten Strömungen, wie beispielsweise die Luftwirbel von Tornados.
Sobald die Forscher solche Wirbelmuster identifiziert haben, behandeln sie diese wie klar abgegrenzte Körper, deren Kräfte aufeinander wirken. So lassen sich die Bewegungsdynamiken in instationären Strömungen verhältnismäßig einfach berechnen. In ihrer Studie simulieren Huhn und Kollegen zwei Szenarien. Das erste ist die gleichförmige Schwimmbewegung, die durch regelmäßige Wirbelbildung begleitet wird. Die zweite Simulation ist eine Fluchtbewegung, auch C-Start genannt. Bei dem begibt sich der Fisch in eine C-Form, aus der er nach außen schnellt und so zügig vorwärts kommt.
Allerdings erweist sich für den Antrieb des C-Starts ein nicht rotierender schneller Strömungsstrahl innerhalb der Wirbelfelder als wesentlich, der sich nicht durch die kohärenten Lagrange’schen Strukturen beschreiben lässt. Beim ersten Szenario hat sich die Herangehensweise der Forscher hingegen bewährt. Bei der gleichmäßigen Bewegung konnten sie die Fortbewegung des Schwimmenden zum großen Teil auf die Impulsübertragung zwischen den separierten Wirbeln und dem Fisch zurückführen.
Quelle: https://www.weltderphysik.de/gebiet/materie/nachrichten/2015/die-physik-zwischen-fisch-und-wasser/